Peterson算法(解决临界区问题)详解
本节说明一个经典的基于软件的临界区问题的解决方案,称为 Peterson 算法。
Peterson 算法提供了解决临界区问题的一个很好的算法,并能说明满足互斥、进步、有限等待等要求的软件设计的复杂性。
Peterson算法适用于两个进程交错执行临界区与剩余区。两个进程为 P0 和 P1。为了方便,当使用 Pi 时,用 Pj 来表示另一个进程,即 j == 1 - i。
Peterson算法要求两个进程共享两个数据项:
在解释了这些数据结构后,就可以分析如图 1 所示的算法。
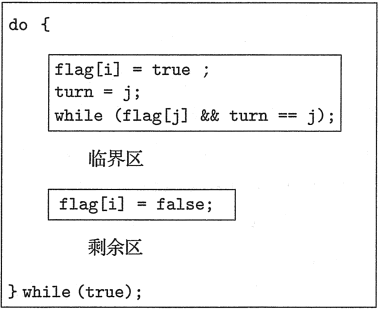
图 1 Perterson算法的进程 Pi 的结构
为了进入临界区,进程 Pi 首先设置 flag[i] 的值为 true;并且设置 turn 的值为 j,从而表示如果另一个进程 Pj 希望进入临界区,那么 Pj 能够进入。如果两个进程同时试图进入,那么 turn 会几乎在同时设置成 i 和 j。只有一个赋值语句的结果会保持;另一个也会设置,但会立即被重写。变量 turn 的最终值决定了哪个进程允许先进入临界区。
现在我们证明这一解答是正确的。这需要证明:
为了证明第 1 点,应注意到,只有当 flag[j] == false 或者 turn == i 时,进程 Pi 才能进入临界区。而且注意,如果两个进程同时在临界区内执行,那么 flag[0]==flag[1]==true。这两点意味着,P0 和 P1 不可能同时成功地执行它们的 while 语句,因为 turn 的值只可能为 0 或 1,而不可能同时为两个值。
因此,只有一个进程如 Pj,能成功地执行完 while 语句,而进程 Pi 应至少再一次执行语句(“turn == j”)。而且,只要在临界区内,flag[j]==true 和 turn==j 就同时成立。结果,互斥成立。
为了证明第 2 点和第 3 点,应注意到,只有条件 flag[j]==true 和 turn==j 成立,进程 Pi 才会陷入 while 循环语句,且 Pi 就能被阻止进入临界区。如果 Pj 不准备进入临界区,那么 flag[j] == false,Pi 能进入临界区。如果 Pj 已设置 flag[j] 为 true 且也在执行 while 语句,那么 turn == j 或 turn == i。如果 turn == i,那么 Pi 进入临界区。如果 turn == j,那么 Pj 进入临界区。
然而,当 Pj 退出临界区时,它会设置 flag[j] 为 false,以允许 Pi 进入临界区。如果 Pj 重新设置 flag[j] 为 true,那么它也应设置 turn 为 i。因此由于进程 Pi 执行 while 语句时并不改变变量 turn 的值,所以 Pi 会进入临界区(进步),而且 Pi 在 Pj 进入临界区后最多一次就能进入(有限等待)。
Peterson 算法提供了解决临界区问题的一个很好的算法,并能说明满足互斥、进步、有限等待等要求的软件设计的复杂性。
Peterson算法适用于两个进程交错执行临界区与剩余区。两个进程为 P0 和 P1。为了方便,当使用 Pi 时,用 Pj 来表示另一个进程,即 j == 1 - i。
Peterson算法要求两个进程共享两个数据项:
int turn;
boolean flag[2];
在解释了这些数据结构后,就可以分析如图 1 所示的算法。

图 1 Perterson算法的进程 Pi 的结构
为了进入临界区,进程 Pi 首先设置 flag[i] 的值为 true;并且设置 turn 的值为 j,从而表示如果另一个进程 Pj 希望进入临界区,那么 Pj 能够进入。如果两个进程同时试图进入,那么 turn 会几乎在同时设置成 i 和 j。只有一个赋值语句的结果会保持;另一个也会设置,但会立即被重写。变量 turn 的最终值决定了哪个进程允许先进入临界区。
现在我们证明这一解答是正确的。这需要证明:
- 互斥成立;
- 进步要求满足;
- 有限等待要求满足;
为了证明第 1 点,应注意到,只有当 flag[j] == false 或者 turn == i 时,进程 Pi 才能进入临界区。而且注意,如果两个进程同时在临界区内执行,那么 flag[0]==flag[1]==true。这两点意味着,P0 和 P1 不可能同时成功地执行它们的 while 语句,因为 turn 的值只可能为 0 或 1,而不可能同时为两个值。
因此,只有一个进程如 Pj,能成功地执行完 while 语句,而进程 Pi 应至少再一次执行语句(“turn == j”)。而且,只要在临界区内,flag[j]==true 和 turn==j 就同时成立。结果,互斥成立。
为了证明第 2 点和第 3 点,应注意到,只有条件 flag[j]==true 和 turn==j 成立,进程 Pi 才会陷入 while 循环语句,且 Pi 就能被阻止进入临界区。如果 Pj 不准备进入临界区,那么 flag[j] == false,Pi 能进入临界区。如果 Pj 已设置 flag[j] 为 true 且也在执行 while 语句,那么 turn == j 或 turn == i。如果 turn == i,那么 Pi 进入临界区。如果 turn == j,那么 Pj 进入临界区。
然而,当 Pj 退出临界区时,它会设置 flag[j] 为 false,以允许 Pi 进入临界区。如果 Pj 重新设置 flag[j] 为 true,那么它也应设置 turn 为 i。因此由于进程 Pi 执行 while 语句时并不改变变量 turn 的值,所以 Pi 会进入临界区(进步),而且 Pi 在 Pj 进入临界区后最多一次就能进入(有限等待)。
所有教程
- socket
- Python基础教程
- C#教程
- MySQL函数
- MySQL
- C语言入门
- C语言专题
- C语言编译器
- C语言编程实例
- GCC编译器
- 数据结构
- C语言项目案例
- C++教程
- OpenCV
- Qt教程
- Unity 3D教程
- UE4
- STL
- Redis
- Android教程
- JavaScript
- PHP
- Mybatis
- Spring Cloud
- Maven
- vi命令
- Spring Boot
- Spring MVC
- Hibernate
- Linux
- Linux命令
- Shell脚本
- Java教程
- 设计模式
- Spring
- Servlet
- Struts2
- Java Swing
- JSP教程
- CSS教程
- TensorFlow
- 区块链
- Go语言教程
- Docker
- 编程笔记
- 资源下载
- 关于我们
- 汇编语言
- 大数据
- 云计算
- VIP视频
