8.5 最小生成树—构造最小生成树的Prim算法
假设G=(V,E)为一网图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。设置两个新的集合U 和T,其中集合U 用于存放G 的最小生成树中的顶点,集合T 存放G 的最小生成树中的边。令集合U 的初值为U={u1}(假设构造最小生成树时,从顶点u1 出发),集合T 的初值为T={}。Prim 算法的思想是,从所有u∈U,v∈V-U 的边中,选取具有最小权值的边(u,v),将顶点v 加入集合U 中,将边(u,v)加入集合T 中,如此不断重复,直到U=V 时,最小生成树构造完毕,这时集合T 中包含了最小生成树的所有边。
Prim 算法可用下述过程描述,其中用wuv 表示顶点u 与顶点v 边上的权值。
(1)U={u1},T={};
(2)while (U≠V)do
(u,v)=min{wuv;u∈U,v∈V-U }
T=T+{(u,v)}
U=U+{v}
(3)结束。
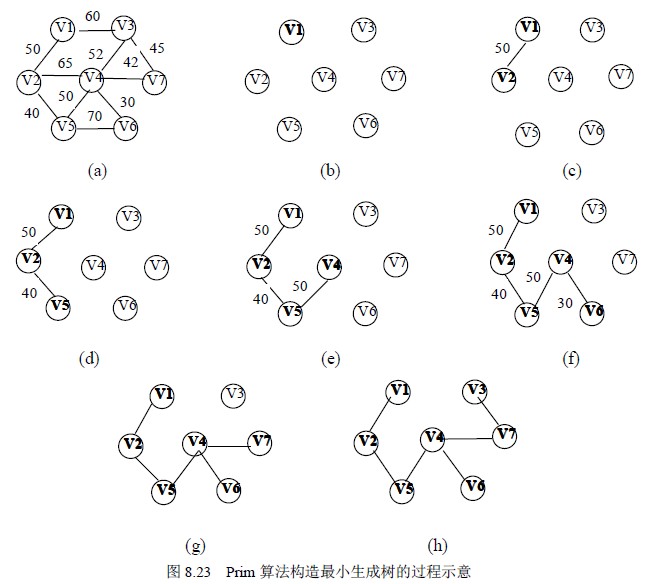
图8.23 (a)所示的一个网图,按照Prim 方法,从顶点1 出发,该网的最小生成树的产生过程如图8.23 (b)、(c)、(d)、(e)、(f)和(g)所示。
为实现Prim 算法,需设置两个辅助一维数组lowcost 和closevert,其中lowcost 用来保存集合V-U 中各顶点与集合U 中各顶点构成的边中具有最小权值的边的权值;数组closevertex 用来保存依附于该边的在集合U 中的顶点。假设初始状态时,U={u1}(u1 为出发的顶点),这时有lowcost[0]=0,它表示顶点u1 已加入集合U 中,数组lowcost 的其它各分量的值是顶点u1 到其余各顶点所构成的直接边的权值。然后不断选取权值最小的边(ui,uk)(ui∈U,uk∈V-U),每选取一条边,就将lowcost(k)置为0,表示顶点uk 已加入集合U 中。由于顶点uk 从集合V-U 进入集合U 后,这两个集合的内容发生了变化,就需依据具体情况更新数组lowcost 和closevertex 中部分分量的内容。最后closevertex 中即为所建立的最小生成树。
当无向网采用二维数组存储的邻接矩阵存储时,Prim 算法的C 语言实现为:
void Prim(int gm[ ][MAXNODE],int n,int closevertex[ ])
{/*用Prim 方法建立有n 个顶点的邻接矩阵存储结构的网图gm 的最小生成树*/
/*从序号为0 的顶点出发;建立的最小生成树存于数组closevertex 中*/
int lowcost[100],mincost;
int i,j,k;
for (i=1;i<n;i++) /*初始化*/
{ lowcost[i]=gm[0][i];
closevertex[i]=0;
}
lowcost[0]=0; /*从序号为0 的顶点出发生成最小生成树*/
closevertex[0]=0;
for (i=1;i<n;i++) /*寻找当前最小权值的边的顶点*/
{mincost=MAXCOST; /*MAXCOST 为一个极大的常量值*/
j=1;k=1;
while (j<n)
{ if (lowcost[j]<mincost && lowcost[j]!=0)
{ mincost=lowcost[j];
k=j;
}
j++;
}
printf(“顶点的序号=%d 边的权值=%d\n”,k,mincost);
lowcost[k]=0;
for (j=1;j<n;j++) /*修改其它顶点的边的权值和最小生成树顶点序号*/
if (gm[k][j]<lowcost[j])
{ lowcost[j]=gm[k][j];
closevertex[j]=k;
}
}
}
算法8.14
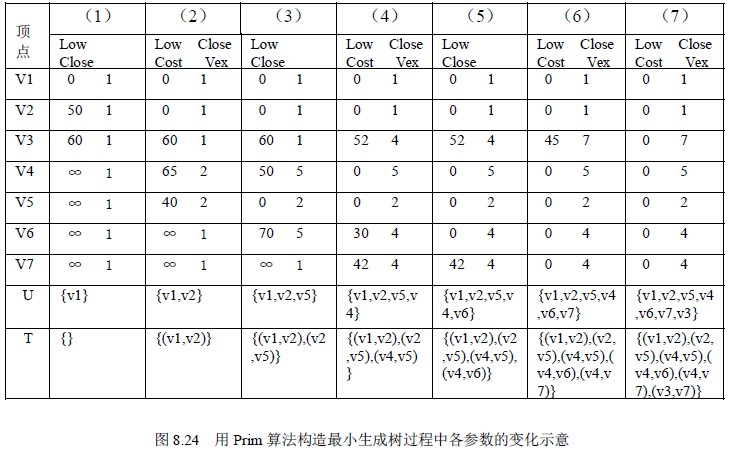
图8.24 给出了在用上述算法构造网图8.23 (a)的最小生成树的过程中,数组closevertex、lowcost 及集合U,V-U 的变化情况,读者可进一步加深对Prim 算法的了解。
在Prim 算法中,第一个for 循环的执行次数为n-1,第二个for 循环中又包括了一个while 循环和一个for 循环,执行次数为2(n-1)2,所以Prim 算法的时间复杂度为O(n2)。
Prim 算法可用下述过程描述,其中用wuv 表示顶点u 与顶点v 边上的权值。
(1)U={u1},T={};
(2)while (U≠V)do
(u,v)=min{wuv;u∈U,v∈V-U }
T=T+{(u,v)}
U=U+{v}
(3)结束。
图8.23 (a)所示的一个网图,按照Prim 方法,从顶点1 出发,该网的最小生成树的产生过程如图8.23 (b)、(c)、(d)、(e)、(f)和(g)所示。

为实现Prim 算法,需设置两个辅助一维数组lowcost 和closevert,其中lowcost 用来保存集合V-U 中各顶点与集合U 中各顶点构成的边中具有最小权值的边的权值;数组closevertex 用来保存依附于该边的在集合U 中的顶点。假设初始状态时,U={u1}(u1 为出发的顶点),这时有lowcost[0]=0,它表示顶点u1 已加入集合U 中,数组lowcost 的其它各分量的值是顶点u1 到其余各顶点所构成的直接边的权值。然后不断选取权值最小的边(ui,uk)(ui∈U,uk∈V-U),每选取一条边,就将lowcost(k)置为0,表示顶点uk 已加入集合U 中。由于顶点uk 从集合V-U 进入集合U 后,这两个集合的内容发生了变化,就需依据具体情况更新数组lowcost 和closevertex 中部分分量的内容。最后closevertex 中即为所建立的最小生成树。
当无向网采用二维数组存储的邻接矩阵存储时,Prim 算法的C 语言实现为:
void Prim(int gm[ ][MAXNODE],int n,int closevertex[ ])
{/*用Prim 方法建立有n 个顶点的邻接矩阵存储结构的网图gm 的最小生成树*/
/*从序号为0 的顶点出发;建立的最小生成树存于数组closevertex 中*/
int lowcost[100],mincost;
int i,j,k;
for (i=1;i<n;i++) /*初始化*/
{ lowcost[i]=gm[0][i];
closevertex[i]=0;
}
lowcost[0]=0; /*从序号为0 的顶点出发生成最小生成树*/
closevertex[0]=0;
for (i=1;i<n;i++) /*寻找当前最小权值的边的顶点*/
{mincost=MAXCOST; /*MAXCOST 为一个极大的常量值*/
j=1;k=1;
while (j<n)
{ if (lowcost[j]<mincost && lowcost[j]!=0)
{ mincost=lowcost[j];
k=j;
}
j++;
}
printf(“顶点的序号=%d 边的权值=%d\n”,k,mincost);
lowcost[k]=0;
for (j=1;j<n;j++) /*修改其它顶点的边的权值和最小生成树顶点序号*/
if (gm[k][j]<lowcost[j])
{ lowcost[j]=gm[k][j];
closevertex[j]=k;
}
}
}
算法8.14
图8.24 给出了在用上述算法构造网图8.23 (a)的最小生成树的过程中,数组closevertex、lowcost 及集合U,V-U 的变化情况,读者可进一步加深对Prim 算法的了解。
在Prim 算法中,第一个for 循环的执行次数为n-1,第二个for 循环中又包括了一个while 循环和一个for 循环,执行次数为2(n-1)2,所以Prim 算法的时间复杂度为O(n2)。


