8.6 最短路径—每一对顶点之间的最短路径
解决这个问题的一个办法是:每次以一个顶点为源点,重复招待迪杰斯特拉算法次。这样,便可求得每一结顶点的最短路径。总的执行时间为O(n3)。
这里要介绍由弗洛伊德(Floyd)提出的另一个算法。这个算法的时间复杂度也是O(n3),但形式上简单些。
弗洛伊德算法仍从图的带权邻接矩阵cost 出发,其基本思想是:
假设求从顶点vi 到vj 的最短路径。如果从vi 到vi 有弧,则从vi 到vj 存在一条长度为edges[i][j]的路径,该路径不一定是最短路径,尚需进行n 次试探。首先考虑路径(vi, v0,vj)是否存在(即判别弧(vi, v0)和(v0, vj)是否存在)。如果存在,则比较(vi, vj)和(vi,v0, vj)的路径长度取长度较短者为从vi 到vj 的中间顶点的序号不大于0 的最短路径。假如在路径上再增加一个顶点v1,也就是说,如果(vi, …, v1)和(v1, …, vj)分别是当前找到的中间顶点的序号不大于0 的最短路径,那么(vi, …, v1, … , vj) 就有可能是从vi 到vj 的中间顶点的序号不大于1 的最短路径。将它和已经得到的从vi 到vj 中间顶点序号不大于0 的最短路径相比较,从中选出中间顶点的序号不大于1 的最短路径之后,再增加一个顶点v2,继续进行试探。依次类推。在一般情况下,若(vi, …, vk)和(vk, …, vj)
分别是从vi 到vk 和从vk 到vj 的中间顶点的序号不大于k-1 的最短路径,则将(vi, …,vk, …, vj)和已经得到的从vi 到vj 且中间顶点序号不大于k-1 的最短路径相比较,其长度较短者便是从vi 到vj 的中间顶点的序号不大于k 的最短路径。这样,在经过n 次比较后,最后求得的必是从vi 到vj 的最短路径。
按此方法,可以同时求得各对顶点间的最短路径。
现定义一个n 阶方阵序列。
从上述计算公式可见,D(1)[i][j]是从vi 到vj 的中间顶点的序号不大于1 的最短路径的长度;D( k)[i][j] 是从vi 到vj 的中间顶点的个数不大于k 的最短路径的长度;D( n-1)[i][j] 就是从vi 到vj 的最短路径的长度。
由此得到求任意两顶点间的最短路径的算法8.18。
void ShortestPath_2 (Mgraph G, PathMatrix *P[],DistancMatrix *D)
{/*用Floyd 算法求有向网G 中各对顶点v 和w 之间的最短路径P[v][w]及其带权长度D[v][w]。*/
/*若P[v][w][u]为TRUE,则u 是从v 到w 当前求得的最短路径上的顶点。*/
for(v=0;v<G.vexnum;++v) /*各对顶点之间初始已知路径及距离*/
for(w=0;w<G,vexnum;++w)
{ D[v][w]=G.arcs[v][w];
for(u=0;u<G,vexnum;++u) P[v][w][u]=FALSE;
if (D[v][w]<INFINITY) /*从v 到w 有直接路径*/
{ P[v][w][v]=TRUE;
}
}
for(u=0; u<G.vexnum; ++u)
for(v=0; v<G.vexnum; ++v)
for(w=0;w<G.vexnum;++w)
if (D[v][u]+D[u][w]<D[v][w]) /*从v 经u 到w 的一条路径更短*/
{D[v][w]=D[v][u]+D[u][w];
for(i=0;i<G.vexnum;++i)
P[v][w][i]=P[v][u][i]||P[u][w][i];
}
}/* ShortestPath_2*/
算法8.18
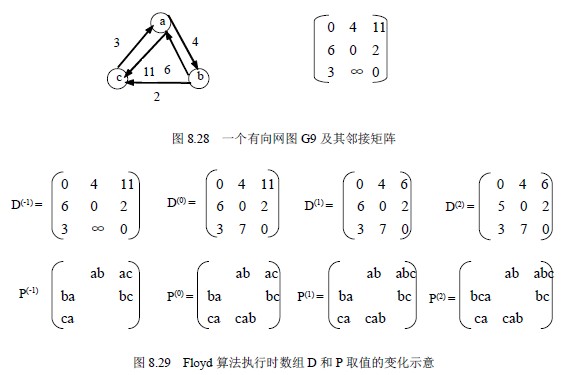
图8.28 给出了一个简单的有向网及其邻接矩阵。图8.29 给出了用Floyd 算法求该有向网中每对顶点之间的最短路径过程中,数组D 和数组P 的变化情况。
这里要介绍由弗洛伊德(Floyd)提出的另一个算法。这个算法的时间复杂度也是O(n3),但形式上简单些。
弗洛伊德算法仍从图的带权邻接矩阵cost 出发,其基本思想是:
假设求从顶点vi 到vj 的最短路径。如果从vi 到vi 有弧,则从vi 到vj 存在一条长度为edges[i][j]的路径,该路径不一定是最短路径,尚需进行n 次试探。首先考虑路径(vi, v0,vj)是否存在(即判别弧(vi, v0)和(v0, vj)是否存在)。如果存在,则比较(vi, vj)和(vi,v0, vj)的路径长度取长度较短者为从vi 到vj 的中间顶点的序号不大于0 的最短路径。假如在路径上再增加一个顶点v1,也就是说,如果(vi, …, v1)和(v1, …, vj)分别是当前找到的中间顶点的序号不大于0 的最短路径,那么(vi, …, v1, … , vj) 就有可能是从vi 到vj 的中间顶点的序号不大于1 的最短路径。将它和已经得到的从vi 到vj 中间顶点序号不大于0 的最短路径相比较,从中选出中间顶点的序号不大于1 的最短路径之后,再增加一个顶点v2,继续进行试探。依次类推。在一般情况下,若(vi, …, vk)和(vk, …, vj)
分别是从vi 到vk 和从vk 到vj 的中间顶点的序号不大于k-1 的最短路径,则将(vi, …,vk, …, vj)和已经得到的从vi 到vj 且中间顶点序号不大于k-1 的最短路径相比较,其长度较短者便是从vi 到vj 的中间顶点的序号不大于k 的最短路径。这样,在经过n 次比较后,最后求得的必是从vi 到vj 的最短路径。
按此方法,可以同时求得各对顶点间的最短路径。
现定义一个n 阶方阵序列。
D(-1),D(0),D(1),…,D(k),D(n-1)
其中
D(-1)[i][j]=edges[i][j]
D( k)[i][j]=Min{D( k-1)[i][j], D( k-1)[i][k]+D( k-1)[k][j]} 0ㄑkㄑn-1
D( k)[i][j]=Min{D( k-1)[i][j], D( k-1)[i][k]+D( k-1)[k][j]} 0ㄑkㄑn-1
从上述计算公式可见,D(1)[i][j]是从vi 到vj 的中间顶点的序号不大于1 的最短路径的长度;D( k)[i][j] 是从vi 到vj 的中间顶点的个数不大于k 的最短路径的长度;D( n-1)[i][j] 就是从vi 到vj 的最短路径的长度。
由此得到求任意两顶点间的最短路径的算法8.18。
void ShortestPath_2 (Mgraph G, PathMatrix *P[],DistancMatrix *D)
{/*用Floyd 算法求有向网G 中各对顶点v 和w 之间的最短路径P[v][w]及其带权长度D[v][w]。*/
/*若P[v][w][u]为TRUE,则u 是从v 到w 当前求得的最短路径上的顶点。*/
for(v=0;v<G.vexnum;++v) /*各对顶点之间初始已知路径及距离*/
for(w=0;w<G,vexnum;++w)
{ D[v][w]=G.arcs[v][w];
for(u=0;u<G,vexnum;++u) P[v][w][u]=FALSE;
if (D[v][w]<INFINITY) /*从v 到w 有直接路径*/
{ P[v][w][v]=TRUE;
}
}
for(u=0; u<G.vexnum; ++u)
for(v=0; v<G.vexnum; ++v)
for(w=0;w<G.vexnum;++w)
if (D[v][u]+D[u][w]<D[v][w]) /*从v 经u 到w 的一条路径更短*/
{D[v][w]=D[v][u]+D[u][w];
for(i=0;i<G.vexnum;++i)
P[v][w][i]=P[v][u][i]||P[u][w][i];
}
}/* ShortestPath_2*/
算法8.18
图8.28 给出了一个简单的有向网及其邻接矩阵。图8.29 给出了用Floyd 算法求该有向网中每对顶点之间的最短路径过程中,数组D 和数组P 的变化情况。


