9.2 静态查找表—有序表的插值查找和斐波那契查找

一.插值查找

插值查找通过下列公式
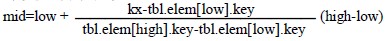
求取中点，其中low 和high 分别为表的两个端点下标，kx 为给定值。
若kx<tbl.elem[mid].key，则high=mid-1，继续左半区查找；
若kx>tbl.elem[mid].key，则low=mid+1，继续右半区查找；
若kx=tbl.elem[mid].key，查找成功。

插值查找是平均性能最好的查找方法，但只适合于关键码均匀分布的表，其时间效率依然是O(log2n)。

二.斐波那契查找

斐波那契查找通过斐波那契数列对有序表进行分割，查找区间的两个端点和中点都与斐波那契数有关。斐波那契数列定义如下： 设n 个数据元素的有序表，且n 正好是某个斐波那契数-1，即n=F(k)-1 时，可用此查找方法。

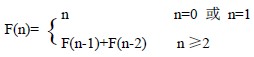
斐波那契查找分割的思想为：对于表长为F(i)-1 的有序表，以相对low 偏移量F(i-1)-1 取中点，即mid=low+F(i-1)-1，对表进行分割，则左子表表长为F(i-1)-1，右子表表长为F(i)-1-[F(i-1)-1]-1=F(i-2)-1。可见，两个子表表长也都是某个斐波那契数-1，因而，可以对子表继续分割。

【算法9.3】
① low=1；high=F(k)-1； // 设置初始区间
F=F(k)-1；f=F(k-1)-1； // F 为表长，f 为取中点的相对偏移量
② 当low>high 时，返回查找失败信息// 表空，查找失败
③ low≤high，mid=low+f; // 取中点
a. 若kx<tbl.elem[mid].key，则
     p=f；f=F-f-1； // 计算取中点的相对偏移量
     F=p； // 调整表长F
     high=mid-1；转② // 查找在左半区进行
b. 若kx>tbl.elem[mid].key，则
    F=F-f-1； // 调整表长F
    f=f-F-1； // 计算取中点的相对偏移量
    low=mid+1；转② // 查找在右半区进行
c. 若kx=tbl.elem[mid].key，返回数据元素在表中位置// 查找成功

当n 很大时，该查找方法称为黄金分割法，其平均性能比折半查找好，但其时间效率仍为O(log2n)，而且，在最坏情况下比折半查找差，优点是计算中点仅作加、减运算。