9.4 哈希表查找(杂凑法)—处理冲突的方法
一. 开放定址法
所谓开放定址法,即是由关键码得到的哈希地址一旦产生了冲突,也就是说,该地址已经存放了数据元素,就去寻找下一个空的哈希地址,只要哈希表足够大,空的哈希地址总能找到,并将数据元素存入。
找空哈希地址方法很多,下面介绍三种:
1. 线性探测法
Hi=(Hash(key)+di) mod m ( 1≤i < m )
其中:
Hash(key)为哈希函数
m 为哈希表长度
di 为增量序列1,2,……,m-1,且di=i
【例9.12】关键码集为{47,7,29,11,16,92,22,8,3},哈希表表长为11,Hash(key)=key mod 11,用线性探测法处理冲突,建表如下:

由H1=(Hash(29)+1) mod 11=8,哈希地址8 为空,将29 存入。另外,22、8 同样在哈希地址上有冲突,也是由H1 找到空的哈希地址的;
而Hash(3)=3,哈希地址上冲突,由
H1=(Hash(3)+1) mod 11=4 仍然冲突;
H2=(Hash(3)+2) mod 11=5 仍然冲突;
H3=(Hash(3)+3) mod 11=6 找到空的哈希地址,存入。
线性探测法可能使第i 个哈希地址的同义词存入第i+1 个哈希地址,这样本应存入第i+1 个哈希地址的元素变成了第i+2 个哈希地址的同义词,……,因此,可能出现很多元素在相邻的哈希地址上“堆积”起来,大大降低了查找效率。为此,可采用二次探测法,或双哈希函数探测法,以改善“堆积”问题。
2. 二次探测法
Hi=(Hash(key)±di) mod m
其中:
Hash(key)为哈希函数
m 为哈希表长度,m 要求是某个4k+3 的质数(k 是整数)
di 为增量序列12,-12,22,-22,……,q2,-q2 且q≤1/2 (m-1)
仍以上例用二次探测法处理冲突,建表如下:

Hash(3)=3,哈希地址上冲突,由
H1=(Hash(3)+12) mod 11=4 仍然冲突;
H2=(Hash(3)-12) mod 11=2 找到空的哈希地址,存入。
3. 双哈希函数探测法
Hi=(Hash(key)+i*ReHash(key)) mod m (i=1,2,……,m-1)
其中:
Hash(key),ReHash(key)是两个哈希函数,
m 为哈希表长度
双哈希函数探测法,先用第一个函数Hash(key)对关键码计算哈希地址,一旦产生地址冲突,再用第二个函数ReHash(key)确定移动的步长因子,最后,通过步长因子序列由探测函数寻找空的哈希地址。
比如,Hash(key)=a 时产生地址冲突,就计算ReHash(key)=b,则探测的地址序列为
H1=(a+b) mod m,H2=(a+2b) mod m,……,Hm-1=(a+(m-1)b) mod m
二. 拉链法
设哈希函数得到的哈希地址域在区间[0,m-1]上,以每个哈希地址作为一个指针,指向一个链,即分配指针数组ElemType *eptr[m];建立m 个空链表,由哈希函数对关键码转换后,映射到同一哈希地址i 的同义词均加入到*eptr[i]指向的链表中。
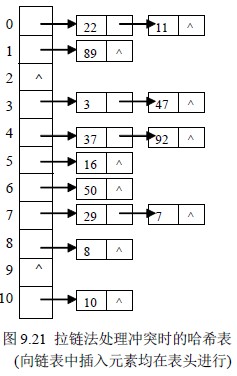
【例9.l3】关键码序列为47,7,29,11,16,92,22,8,3,50,37,89,94,21,哈希函数为Hash(key)=key mod 11
用拉链法处理冲突,建表如图9.21。
三. 建立一个公共溢出区
设哈希函数产生的哈希地址集为[0,m-1],则分配两个表:
一个基本表ElemType base_tbl[m];每个单元只能存放一个元素;
一个溢出表ElemType over_tbl[k];只要关键码对应的哈希地址在基本表上产生冲突,则所有这样的元素一律存入该表中。查找时,对给定值kx 通过哈希函数计算出哈希地址i,先与基本表的base_tbl[i]单元比较,若相等,查找成功;否则,再到溢出表中进行查找。

