10.4选择排序—树形选择排序
按照锦标赛的思想进行,将n 个参赛的选手看成完全二叉树的叶结点,则该完全二叉树有2n-2 或2n-1 个结点。首先,两两进行比赛(在树中是兄弟的进行,否则轮空,直接进入下一轮),胜出的再兄弟间再两两进行比较,直到产生第一名;接下来,将作为第一名的结点看成最差的,并从该结点开始,沿该结点到根路径上,依次进行各分枝结点子女间的比较,胜出的就是第二名。因为和他比赛的均是刚刚输给第一名的选手。如此,继续进行下去,直到所有选手的名次排定。
【例10.6】16 个选手的比赛(n=24)
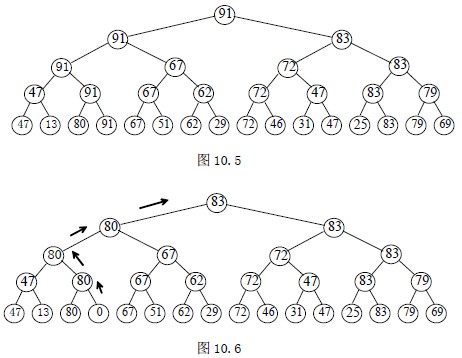
图10.5 中,从叶结点开始的兄弟间两两比赛,胜者上升到父结点;胜者兄弟间再两两比赛,直到根结点,产生第一名91。比较次数为23+22+21+20=24-1=n-1。
图10.6 中,将第一名的结点置为最差的,与其兄弟比赛,胜者上升到父结点,胜者兄弟间再比赛,直到根结点,产生第二名83。比较次数为4,即log2n 次。其后各结点的名次均是这样产生的,所以,对于n 个参赛选手来说,即对n 个记录进行树形选择排序,总的关键码比较次数至多为(n−1)log2n+n−1,故时间复杂度为O(nlog2n)。该方法占用空间较多,除需输出排序结果的n 个单元外,尚需n-1 个辅助单元。
【例10.6】16 个选手的比赛(n=24)

图10.5 中,从叶结点开始的兄弟间两两比赛,胜者上升到父结点;胜者兄弟间再两两比赛,直到根结点,产生第一名91。比较次数为23+22+21+20=24-1=n-1。
图10.6 中,将第一名的结点置为最差的,与其兄弟比赛,胜者上升到父结点,胜者兄弟间再比赛,直到根结点,产生第二名83。比较次数为4,即log2n 次。其后各结点的名次均是这样产生的,所以,对于n 个参赛选手来说,即对n 个记录进行树形选择排序,总的关键码比较次数至多为(n−1)log2n+n−1,故时间复杂度为O(nlog2n)。该方法占用空间较多,除需输出排序结果的n 个单元外,尚需n-1 个辅助单元。

