10.4选择排序—堆排序(Heap Sort)
设有n 个元素的序列k1,k2,…,kn,当且仅当满足下述关系之一时,称之为堆。
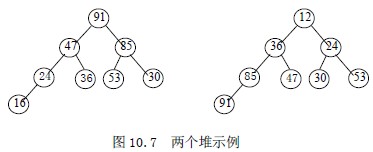
若以一维数组存储一个堆,则堆对应一棵完全二叉树,且所有非叶结点的值均不大于(或不小于)其子女的值,根结点的值是最小(或最大)的。
设有n 个元素,将其按关键码排序。首先将这n 个元素按关键码建成堆,将堆顶元素输出,得到n 个元素中关键码最小(或最大)的元素。然后,再对剩下的n-1 个元素建成堆,输出堆顶元素,得到n 个元素中关键码次小(或次大)的元素。如此反复,便得到一个按关键码有序的序列。称这个过程为堆排序。
因此,实现堆排序需解决两个问题:
1. 如何将n 个元素的序列按关键码建成堆;
2. 输出堆顶元素后,怎样调整剩余n-1 个元素,使其按关键码成为一个新堆。
首先,讨论输出堆顶元素后,对剩余元素重新建成堆的调整过程。
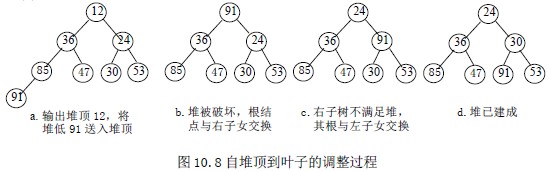
调整方法:设有m 个元素的堆,输出堆顶元素后,剩下m-1 个元素。将堆底元素送入堆顶,堆被破坏,其原因仅是根结点不满足堆的性质。将根结点与左、右子女中较小(或小大)的进行交换。若与左子女交换,则左子树堆被破坏,且仅左子树的根结点不满足堆的性质;若与右子女交换,则右子树堆被破坏,且仅右子树的根结点不满足堆的性质。继续对不满足堆性质的子树进行上述交换操作,直到叶子结点,堆被建成。称这个自根结点到叶子结点的调整过程为筛选。
【例10.6】
 再讨论对n 个元素初始建堆的过程。
再讨论对n 个元素初始建堆的过程。
建堆方法:对初始序列建堆的过程,就是一个反复进行筛选的过程。n 个结点的完全二叉树,则最后一个结点是第个结点的子女。对第个结点为根的子树筛选,子树成为堆,之后向前依次对各结点为根的子树进行筛选,使之成为堆,直到根结点。
【例10.7】
堆排序:对n 个元素的序列进行堆排序,先将其建成堆,以根结点与第n 个结点交换;
调整前n-1 个结点成为堆,再以根结点与第n-1 个结点交换;重复上述操作,直到整个序列有序。
【算法10.10】
void HeapAdjust(S_TBL *h,int s,int m)
{/*r[s…m]中的记录关键码除r[s]外均满足堆的定义,本函数将对第s 个结点为根的子树筛选,使其成为大顶堆*/
rc=h->r[s];
for(j=2*s;j<=m;j=j*2) /* 沿关键码较大的子女结点向下筛选*/
{ if(j<m&&h->r[j].key<h->r[j+1].key)
j=j+1; /* 为关键码较大的元素下标*/
if(rc.key<h->r[j].key) break; /* rc 应插入在位置s 上*/
h->r[s]=h->r[j]; s=j; /* 使s 结点满足堆定义*/
}
h->r[s]=rc; /* 插入*/
}
void HeapSort(S_TBL *h)
{ for(i=h->length/2;i>0;i--) /* 将r[1..length]建成堆*/
HeapAdjust(h,i,h->length);
for(i=h->length;i>1;i--)
{ h->r[1]<-->h->r[i]; /* 堆顶与堆低元素交换*/
HeapAdjust(h,1,i-1); /*将r[1..i-1]重新调整为堆*/
}
}
【效率分析】
设树高为k,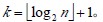 从根到叶的筛选,关键码比较次数至多2(k-1)次,交换记录至多k 次。所以,在建好堆后,排序过程中的筛选次数不超过下式:
从根到叶的筛选,关键码比较次数至多2(k-1)次,交换记录至多k 次。所以,在建好堆后,排序过程中的筛选次数不超过下式:

若以一维数组存储一个堆,则堆对应一棵完全二叉树,且所有非叶结点的值均不大于(或不小于)其子女的值,根结点的值是最小(或最大)的。
设有n 个元素,将其按关键码排序。首先将这n 个元素按关键码建成堆,将堆顶元素输出,得到n 个元素中关键码最小(或最大)的元素。然后,再对剩下的n-1 个元素建成堆,输出堆顶元素,得到n 个元素中关键码次小(或次大)的元素。如此反复,便得到一个按关键码有序的序列。称这个过程为堆排序。
因此,实现堆排序需解决两个问题:
1. 如何将n 个元素的序列按关键码建成堆;
2. 输出堆顶元素后,怎样调整剩余n-1 个元素,使其按关键码成为一个新堆。
首先,讨论输出堆顶元素后,对剩余元素重新建成堆的调整过程。
调整方法:设有m 个元素的堆,输出堆顶元素后,剩下m-1 个元素。将堆底元素送入堆顶,堆被破坏,其原因仅是根结点不满足堆的性质。将根结点与左、右子女中较小(或小大)的进行交换。若与左子女交换,则左子树堆被破坏,且仅左子树的根结点不满足堆的性质;若与右子女交换,则右子树堆被破坏,且仅右子树的根结点不满足堆的性质。继续对不满足堆性质的子树进行上述交换操作,直到叶子结点,堆被建成。称这个自根结点到叶子结点的调整过程为筛选。
【例10.6】

建堆方法:对初始序列建堆的过程,就是一个反复进行筛选的过程。n 个结点的完全二叉树,则最后一个结点是第个结点的子女。对第个结点为根的子树筛选,子树成为堆,之后向前依次对各结点为根的子树进行筛选,使之成为堆,直到根结点。
【例10.7】
堆排序:对n 个元素的序列进行堆排序,先将其建成堆,以根结点与第n 个结点交换;
调整前n-1 个结点成为堆,再以根结点与第n-1 个结点交换;重复上述操作,直到整个序列有序。
【算法10.10】
void HeapAdjust(S_TBL *h,int s,int m)
{/*r[s…m]中的记录关键码除r[s]外均满足堆的定义,本函数将对第s 个结点为根的子树筛选,使其成为大顶堆*/
rc=h->r[s];
for(j=2*s;j<=m;j=j*2) /* 沿关键码较大的子女结点向下筛选*/
{ if(j<m&&h->r[j].key<h->r[j+1].key)
j=j+1; /* 为关键码较大的元素下标*/
if(rc.key<h->r[j].key) break; /* rc 应插入在位置s 上*/
h->r[s]=h->r[j]; s=j; /* 使s 结点满足堆定义*/
}
h->r[s]=rc; /* 插入*/
}
void HeapSort(S_TBL *h)
{ for(i=h->length/2;i>0;i--) /* 将r[1..length]建成堆*/
HeapAdjust(h,i,h->length);
for(i=h->length;i>1;i--)
{ h->r[1]<-->h->r[i]; /* 堆顶与堆低元素交换*/
HeapAdjust(h,1,i-1); /*将r[1..i-1]重新调整为堆*/
}
}
【效率分析】
设树高为k,
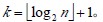 从根到叶的筛选,关键码比较次数至多2(k-1)次,交换记录至多k 次。所以,在建好堆后,排序过程中的筛选次数不超过下式:
从根到叶的筛选,关键码比较次数至多2(k-1)次,交换记录至多k 次。所以,在建好堆后,排序过程中的筛选次数不超过下式:
2( ⎣log2(n−1)⎦ + ⎣log2(n−2)⎦ + … + log22⎦ ) < 2nlog2n
而建堆时的比较次数不超过4n 次,因此堆排序最坏情况下,时间复杂度也为O(nlog2n)。
