10.7.1 外排序—多路平衡归并的实现
从上式可见，增加k 可以减少s，从而减少外存读/写的次数。但是，从下面的讨论中又可发现，单纯增加k 将导致增加内部归并的时间utmg。那末，如何解决这个矛盾呢？
先看2-路归并。令u 个记录分布在两个归并段上，按Merge 函数进行归并。每得到归并后的含u 个记录的归并段需进行u-1 次比较。
再看k-路归并。令u 个记录分布在k 个归并段上，显然，归并后的第一个记录应是k个归并段中关键码最小的记录，即应从每个归并段的第一个记录的相互比较中选出最小者，这需要进行k-1 次比较。同理，每得到归并后的有序段中的一个记录，都要进行k-1 次比较。显然，为得到含u 个记录的归并段需进行(u-1)(k-1)次比较。由此，对n 个记录的文件进行外部排序时，在内部归并过程中进行的总的比较次数为s(k-1)(n-1)。假设所得初始归并段为m 个，则可得内部归并过程中进行比较的总的次数为
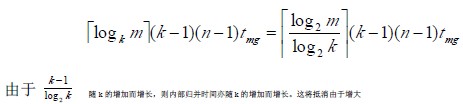k 而减少外存信息读写时间所得效益，这是我们所不希望的。然而，若在进行k-路归并时利用“败者树”(Tree of Loser)，则可使在k 个记录中选出关键码最小的记录时仅需进它不再随k 的增长而增长。
何谓“败者树”？它是树形选择排序的一种变型。相对地，我们可称图10.5 和图10.6中二叉树为“胜者树”，因为每个非终端结点均表示其左、右子女结点中“胜者”。反之，若在双亲结点中记下刚进行完的这场比赛中的败者，而让胜者去参加更高一层的比赛，便可得到一棵“败者树”。
【例10.9】
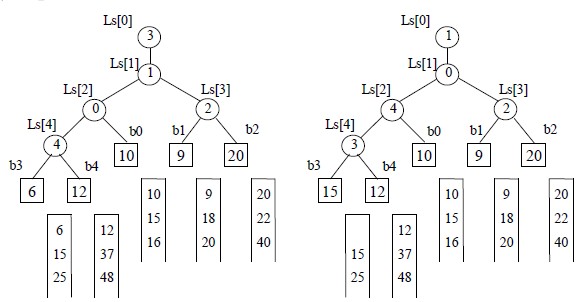
图10.13(a)即为一棵实现5-路归并的败者树ls[0…4]，图中方形结点表示叶子结点(也可看成是外结点)，分别为5 个归并段中当前参加归并的待选择记录的关键码；败者树中根结点ls[1]的双亲结点ls[0]为“冠军”，在此指示各归并段中的最小关键码记录为第三段中的记录；结点ls[3]指示b1 和b2 两个叶子结点中的败者即是b2，而胜者b1 和b3(b3 是叶子结点b3、b4 和b0 经过两场比赛后选出的获胜者)进行比较，结点ls[1]则指示它们中的败者为b1。在选得最小关键码的记录之后，只要修改叶子结点b3 中的值，使其为同一归并段中的下一个记录的关键码，然后从该结点向上和双亲结点所指的关键码进行比较，败者留在该双亲，胜者继续向上直至树根的双亲。如图10.13(b)所示。当第3 个归并段中第2个记录参加归并时，选得最小关键码记录为第一个归并段中的记录。为了防止在归并过程中某个归并段变为空，可以在每个归并段中附加一个关键码为最大的记录。当选出的“冠军”记录的关键码为最大值时，表明此次归并已完成。由于实现k-路归并的败者树
的初始化也容易实现，只要先令所有的非终端结点指向一个含最小关键码的叶子结点，然后从各叶子结点出发调整非终端结点为新的败者即可。
下面程序中简单描述了利用败者树进行k-路归并的过程，为了突出如何利用败者树进行归并，避开了外存信息存取的细节，可以认为归并段已存在。
【算法10.15】
typedef int LoserTree[k]; /*败者树是完全二叉树且不含叶子，可采用顺序存储结构*/
typedef struct{
KeyType key;
}ExNode,External[k]; /*外结点，只存放待归并记录的关键码*/
void K_Merge(LoserTree *ls,External *b) /*k-路归并处理程序*/
{ /*利用败者树ls 将编号从0 到k-1 的k 个输入归并段中的记录归并到输出归并段*/
/*b[0]到b[k-1]为败者树上的k 个叶子结点，分别存放k 个输入归并段中当前记录的关键码*/
for(i=0;i<k;i++) input(b[i].key); /*分别从k 个输入归并段读入该段当前第一个记录的*/
/*关键码到外结点*/
CreateLoserTree(ls); /*建败者树ls，选得最小关键码为b[0].key*/
while(b[ls[0]].key!=MAXKEY)
{ q=ls[0]; /*q 指示当前最小关键码所在归并段*/
output(q); /*将编号为q 的归并段中当前(关键码为b[q].key 的记录写至输出归并段)*/
input(b[q].key); /*从编号为q 的输入归并段中读入下一个记录的关键码*/
Adjust(ls,q); /*调整败者树，选择新的最小关键码*/
}
output(ls[0]); /*将含最大关键码MAXKEY 的记录写至输出归并段*/
}
void Adjust(LoserTree *ls,int s) /*选得最小关键码记录后，从叶到根调整败者树，选下一个最小关键码*/
{ /*沿从叶子结点b[s]到根结点ls[0]的路径调整败者树*/
t=(s+k)/2; /*ls[t]是b[s]的双亲结点*/
while(t>0)
{ if(b[s].key>b[ls[t]].key) s<-->ls[t]; /*s 指示新的胜者*/
t=t/2;
}
ls[0]=s;
}
void CreateLoserTree(LoserTree *ls) /*建立败者树*/
{ /*已知b[0]到b[k-1]为完全二叉树ls 的叶子结点存有k 个关键码，沿从叶子到根的k 条路径*/
/*将ls 调整为败者树*/
b[k].key=MINKEY; /*设MINKEY 为关键码可能的最小值*/
for(i=0;i<k;i++) ls[i]=k; /*设置ls 中“败者”的初值*/
for(i=k-1;k>0;i--) Adjust(ls,i); /*依次从b[k-1],b[k-2],…,b[0]出发调整败者*/
}
最后要提及一点，k 值的选择并非越大越好，如何选择合适的k 是一个需要综合考虑的问题。
先看2-路归并。令u 个记录分布在两个归并段上，按Merge 函数进行归并。每得到归并后的含u 个记录的归并段需进行u-1 次比较。
再看k-路归并。令u 个记录分布在k 个归并段上，显然，归并后的第一个记录应是k个归并段中关键码最小的记录，即应从每个归并段的第一个记录的相互比较中选出最小者，这需要进行k-1 次比较。同理，每得到归并后的有序段中的一个记录，都要进行k-1 次比较。显然，为得到含u 个记录的归并段需进行(u-1)(k-1)次比较。由此，对n 个记录的文件进行外部排序时，在内部归并过程中进行的总的比较次数为s(k-1)(n-1)。假设所得初始归并段为m 个，则可得内部归并过程中进行比较的总的次数为
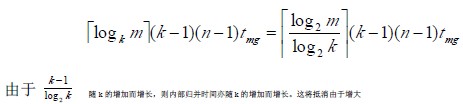
何谓“败者树”？它是树形选择排序的一种变型。相对地，我们可称图10.5 和图10.6中二叉树为“胜者树”，因为每个非终端结点均表示其左、右子女结点中“胜者”。反之，若在双亲结点中记下刚进行完的这场比赛中的败者，而让胜者去参加更高一层的比赛，便可得到一棵“败者树”。
【例10.9】
的初始化也容易实现，只要先令所有的非终端结点指向一个含最小关键码的叶子结点，然后从各叶子结点出发调整非终端结点为新的败者即可。
下面程序中简单描述了利用败者树进行k-路归并的过程，为了突出如何利用败者树进行归并，避开了外存信息存取的细节，可以认为归并段已存在。
【算法10.15】
typedef int LoserTree[k]; /*败者树是完全二叉树且不含叶子，可采用顺序存储结构*/
typedef struct{
KeyType key;
}ExNode,External[k]; /*外结点，只存放待归并记录的关键码*/
void K_Merge(LoserTree *ls,External *b) /*k-路归并处理程序*/
{ /*利用败者树ls 将编号从0 到k-1 的k 个输入归并段中的记录归并到输出归并段*/
/*b[0]到b[k-1]为败者树上的k 个叶子结点，分别存放k 个输入归并段中当前记录的关键码*/
for(i=0;i<k;i++) input(b[i].key); /*分别从k 个输入归并段读入该段当前第一个记录的*/
/*关键码到外结点*/
CreateLoserTree(ls); /*建败者树ls，选得最小关键码为b[0].key*/
while(b[ls[0]].key!=MAXKEY)
{ q=ls[0]; /*q 指示当前最小关键码所在归并段*/
output(q); /*将编号为q 的归并段中当前(关键码为b[q].key 的记录写至输出归并段)*/
input(b[q].key); /*从编号为q 的输入归并段中读入下一个记录的关键码*/
Adjust(ls,q); /*调整败者树，选择新的最小关键码*/
}
output(ls[0]); /*将含最大关键码MAXKEY 的记录写至输出归并段*/
}
void Adjust(LoserTree *ls,int s) /*选得最小关键码记录后，从叶到根调整败者树，选下一个最小关键码*/
{ /*沿从叶子结点b[s]到根结点ls[0]的路径调整败者树*/
t=(s+k)/2; /*ls[t]是b[s]的双亲结点*/
while(t>0)
{ if(b[s].key>b[ls[t]].key) s<-->ls[t]; /*s 指示新的胜者*/
t=t/2;
}
ls[0]=s;
}
void CreateLoserTree(LoserTree *ls) /*建立败者树*/
{ /*已知b[0]到b[k-1]为完全二叉树ls 的叶子结点存有k 个关键码，沿从叶子到根的k 条路径*/
/*将ls 调整为败者树*/
b[k].key=MINKEY; /*设MINKEY 为关键码可能的最小值*/
for(i=0;i<k;i++) ls[i]=k; /*设置ls 中“败者”的初值*/
for(i=k-1;k>0;i--) Adjust(ls,i); /*依次从b[k-1],b[k-2],…,b[0]出发调整败者*/
}
最后要提及一点，k 值的选择并非越大越好，如何选择合适的k 是一个需要综合考虑的问题。
