算法及其时间复杂度和空间复杂度的习题
一、单项选择题
1.个算法应该是( )。A.程序 B.问题求解步骤的描述 C.要满足五个基本特性 D. A和C
2.某算法的时间复杂度为O(n2),表明该算法的( )。
A.问题规模是n2 B.执行时间等于n2
C.执行时间与n2成正比 D.问题规模与n2成正比
3.以下算法的时间复杂度为( )。
void fun(int n) {
int i=l;
while(i<=n)
i=i*2;
}
A. O(n) B. O(n2) C. O(nlog2n) D. O(log2n)4.【2011年计算机联考真题】
设n是描述问题规模的非负整数,下面程序片段的时间复杂度是()。
x=2;
while(x<n/2)
x=2*x;
A. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)5.【2012年计算机联考真题】
求整数n (n>=0)阶乘的算法如下,其时间复杂度是( )。
int fact(int n){
if (n<=l) return 1;
return n*fact(n-1);
}
A. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)6.有以下算法,其时间复杂度为( )。
void fun (int n){
int i=0;
while(i*i*i<=n)
i++;
}
A. O(n) B. O(nlogn) C. 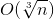 D.
D. 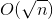
7.程序段
for(i=n-l;i>l;i--)
for(j=1;j<i;j++)
if (A[j]>A[j+l])
A[j]与 A[j+1]对换;
其中n为正整数,则最后一行的语句频度在最坏情况下是( )。A. O(n) B. O(nlogn) C. O(n3) D. O(n2)
8.以下算法中加下划线语句的执行次数为()。
int m=0, i, j;
for(i=l;i<=n;i++)
for(j=1;j<=2 * i;j++)
m++;
A. n(n+1) B. n C. n+1 D. n29.下面说法错误的是( )。
Ⅰ.算法原地工作的含义是指不需要任何额外的辅助空间
Ⅱ.在相同的规模n下,复杂度O(n)的算法在时间上总是优于复杂度O(2n)的算法
Ⅲ.所谓时间复杂度是指最坏情况下,估算算法执行时间的一个上界
Ⅳ.同一个算法,实现语言的级别越高,执行效率就越低
A. Ⅰ B. Ⅰ、Ⅱ C. Ⅰ、Ⅳ D. Ⅲ
二、综合应用题
1.一个算法所需时间由下述递归方程表示,试求出该算法的时间复杂度的级别(或阶)。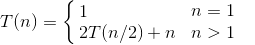
式中,n是问题的规模,为简单起见,设n是2的整数幂。
2.分析以下各程序段,求出算法的时间复杂度。
// 程序段①
i=l;k=0;
while(i<n-l){
k=k+10*i;
i++;
}
// 程序段②
y=0;
while((y+1)*(y+1)<=n)
y=y+1;
// 程序段③
for(i=l;i<=n;i++)
for(j =1;j <=i;j ++)
for(k=l;k<=j;k++)
x++;
// 程序段④
for(i=0;i<n;i++)
for(j=0;j<m;j++)
a[i] [j]=0;
答案与解析
一、单项选择题
1. B程序不一定满足有穷性,如死循环、操作系统等,而算法必须有穷。算法代表了对问题求解步骤的描述,而程序则是算法在计算机上的特定的实现。
2. C
时间复杂度为O(n2),说明算法的执行时间T(n)<=c * n2(c为比例常数),即T(n)=O(n2),时间复杂度T(n)是问题规模n的函数,其问题规模仍然是n而不是n2。
3. D
基本运算是i=i*2,设其执行时间为T(n),则2T(n)<=n,即T(n)<=log2n=O(log2n)。
4. A
在程序中,执行频率最高的语句为“x=2*x”。设该语句共执行了 t次,则2t+1=n/2,故t=log2(n/2)-1=log2n-2,得 T(n)=O(log2n)。
5. B
本题是求阶乘n!的递归代码,即n*(n-1)*...*1共执行n次乘法操作,故T(n)=O(n)。
6. C
算法的基本运算是i++,设其执行时间为T(n),则有,T(6)*T(n)*T(n)<=n,即T(n)3<=n。故有,
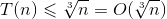 。
。更加直观和快速的解题方法:要计算语句i++的执行次数(由于每执行一次i加1),其中判断条件可理解为i3=n,即
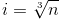 ,因此有
,因此有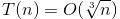 。
。7. D
当所有相邻元素都为逆序时,则最后一行的语句每次都会执行。此时,
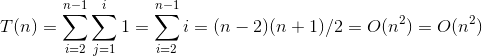
所以在最坏情况下的该语句频度是O(n2)。
8. A
m++语句的执行次数为
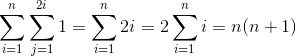
9. A
Ⅰ,算法原地工作是指算法所需的辅助空间是常量。Ⅱ,题中是指算法的时间复杂度,不要想当然认为是程序(该算法的实现)的具体执行时间,而赋予n—个特殊的值。时间复杂度为O(n)的算法,必然总是优于时间复杂度为O(2n)的算法。Ⅲ,时间复杂度总是考虑在最坏情况下的时间复杂度,以保证算法的运行时间不会比它更长。Ⅳ为严蔚敏教材的原话。
二、综合应用题
1.解答:时间复杂度为O(nlog2n)。
设n=2k(k>=0),根据题目所给定义,有
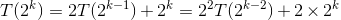 ,由此,可得一般递推公式
,由此,可得一般递推公式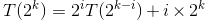 ,进而,可得
,进而,可得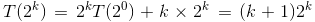 ,即
,即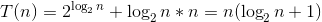 ,即为
,即为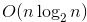 。
。2.解答:
①基本语句是k=k+10*i,共执行了n-2次,所以T(n)=O(n)。
②设循环体共执行T(n)次,每循环一次,循环变量y加1,最终T(n)=y。故(T(n))2<=n,解得 T(n)=O(n1/2)。
③ x++是基本语句,
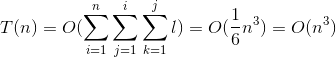 。
。④a[i][j]=0是基本语句,内循环执行m次,外循环执行n次,共执行了 m*n次,所以 T(m, n)=O(m*n)0

