数据结构基础知识总结,时间复杂度是重点
本章的重点是分析程序的时间复杂度。一定要掌握分析时间复杂度的方法和步骤,很多同学在做题时一眼就能看出程序的时间复杂度,但就是无法将其推导过程规范地表述出来。为此,编者查阅众多资料,总结出此类题型的两种形式,供大家参考:
程序①中,i乘以2的次数正是主体语句的执行次数T(n),因此有2T(n)<=n,取对数后,即得 T(n)<=log2n。
程序②中,y加1的次数恰好与T(n)成正比,则令T(n)=y-5,即y=T(n)+5,(T(n)+5+1) *(T(n)+ 5+1)<n,得出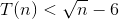 ,即
,即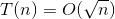 。
。
递归程序一般使用公式进行递推。例如习题5的时间复杂度分析如下:
T(n)=1+T(n-1)=1+1+T(n- 2)=...=n-1+T(1)
即 T(n)=O(n)。
非递归程序比较简单,可以直接累计次数。例如习题7、8等。
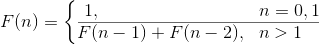
有两种常用的算法:递归算法和非递归算法。试分别分析两种算法的时间复杂度。
(提示:请结合归纳总结中的两种方法进行解答。)
一是循环主体中的变量参与循环条件的判断。
此类题应该找出主体语句中与T(n)成正比的循环变量,将之带入条件中进行计算。例如:// 程序① int i=1; while (i<=n) i=i*2; // 程序② int y=5; while((y+1)*(y+1)<n) y=y+1;
程序①中,i乘以2的次数正是主体语句的执行次数T(n),因此有2T(n)<=n,取对数后,即得 T(n)<=log2n。
程序②中,y加1的次数恰好与T(n)成正比,则令T(n)=y-5,即y=T(n)+5,(T(n)+5+1) *(T(n)+ 5+1)<n,得出
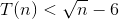 ,即
,即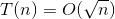 。
。
二是循环主体中的变量与循环条件无关。
此类题可采用数学归纳法,或直接累计循环次数;多层循环时从内到外分析,忽略单步语句、条件判断语句,只关注主体语句的执行次数。此类问题又可分为递归程序和非递归程序。递归程序一般使用公式进行递推。例如习题5的时间复杂度分析如下:
T(n)=1+T(n-1)=1+1+T(n- 2)=...=n-1+T(1)
即 T(n)=O(n)。
非递归程序比较简单,可以直接累计次数。例如习题7、8等。
思维拓展
求解斐波那契数列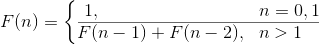
有两种常用的算法:递归算法和非递归算法。试分别分析两种算法的时间复杂度。
(提示:请结合归纳总结中的两种方法进行解答。)

