单链表的操作:节点查找、节点插入、节点删除、求单链表长度
本节讲解一下单链表中节点的查找、插入、删除、求单链表长度等操作。
按序号查找结点值的算法如下:
算法首先调用上面的按序号查找算法GetElem(L, i-1),查找第i-1个结点。假设返回的第i-1个结点为*p,然后令新结,点*s的指针域指向*p的后继结点,再令结点*p的指针域指向新插入的结点*s。其操作过程如图2-6所示。
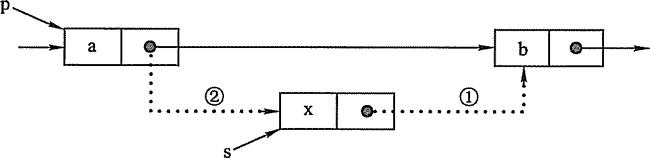
图2-6 单链表的插入操作
实现插入结点的代码片段如下:
扩展:对某一结点进行前插操作
前插操作是指在某结点的前面插入一个新结点,后插操作的定义刚好与之相反,在单链表插入算法中,通常都是釆用后插操作的。
以上面的算法为例,首先调用函数GetElem()找到第i-1个结点,即待插入结点的前驱结点后,再对其执行后插操作。由此可知,对结点的前插操作均可以转化为后插操作,前提是从单链表的头结点开始顺序查找到其前驱结点,时间复杂度为O(n)。
此外,可以釆用另一种方式将其转化为后插操作来实现,设待插入结点为*s,将插入到*p的前面。我们仍然将*s插入到*p的后面,然后将p->data与s->data交换即可,这样既满足了逻辑关系,又能使得时间复杂度为O(1)。算法的代码片段如下:
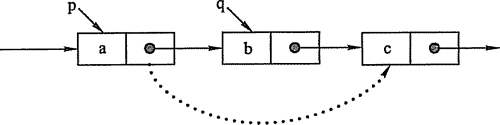
图2-7 单链表结点的删除
假设结点*p为找到的被删结点的前驱结点,为了实现这一操作后的逻辑关系的变化,仅需修改*p的指针域,即将*p的指针域next指向*q的下一结点。
实现删除结点的代码片段如下:
扩展:删除结点*p
要实现删除某一个给定结点*p,通常的做法是先从链表的头结点开始顺序找到其前驱结点,然后再执行删除操作即可,算法的时间复杂度为O(n)。
其实,删除结点*p的操作可以用删除*p的后继结点操作来实现,实质就是将其后继结点的值赋予其自身,然后删除后继结点,也能使得时间复杂度为O(1)。
实现上述操作的代码片段如下:
需要注意的是,因为单链表的长度是不包括头结点的,因此,不带头结点和带头结点的单链表在求表长操作上会略有不同。对不带头结点的单链表,当表为空时,要单独处理。
单链表是整个链表的基础,读者一定要熟练掌握单链表的基本操作算法,在设计算法时,建议先通过图示的方法理清算法的思路,然后再进行算法的编写。
按序号查找结点值
在单链表中从第一个结点出发,顺指针next域逐个往下搜索,直到找到第i个结点为止,否则返回最后一个结点指针域NULL。按序号查找结点值的算法如下:
LNode GetElem(LinkList L,int i){
//本算法取出单链表L(带头结点)中第i个位置的结点指针
int j=1; //计数,初始为1
LNode *p = L->next; //头结点指针赋给p
if(i==0)
return L; //若i等于0,则返回头结点
if(i<1)
return NULL; //若 i 无效,则返回 NULL
while( p && j<i ) { //从第1个结点开始找,查找第i个结点
p=p->next;
j++;
}
return p; //返回第i个结点的指针,如果i大于表长,p=NULL,直接返回p即可
}
按序号查找操作的时间复杂度为O(n)。
按值查找表结点
从单链表第一个结点开始,由前往后依次比较表中各结点数据域的值,若某结点数据域的值等于给定值e,则返回该结点的指针。若整个单链表中没有这样的结点,则返回NULL。按值查找结点的算法如下:
LNode *LocateElem (LinkList L, ElemType e) {
//本算法查找单链表 L (带头结点)中数据域值等于e的结点指针,否则返回NULL
LNode *p=L->next;
while( p!=NULL && p->data!=e) //从第1个结点开始查找data域为e的结点
p=p->next;
return p; //找到后返回该结点指针,否则返回NULL
}
按值查找操作的时间复杂度为O(n)。
插入结点操作
插入操作是将值为x的新结点插入到单链表的第i个位置上。先检查插入位置的合法性,然后找到待插入位置的前驱结点,即第i-1个结点,再在其后插入新结点。算法首先调用上面的按序号查找算法GetElem(L, i-1),查找第i-1个结点。假设返回的第i-1个结点为*p,然后令新结,点*s的指针域指向*p的后继结点,再令结点*p的指针域指向新插入的结点*s。其操作过程如图2-6所示。

图2-6 单链表的插入操作
实现插入结点的代码片段如下:
p=GetElem(L, i-1) ; // 语句①,查找插入位置的前驱结点 s->next=p->next; // 语句②,图 2-6 中辑作步骤 1 p->next=s; // 语句③,图2-6中操作步骤2算法中,语句②③的顺序不能颠倒,否则,当先执行p->next=s后,指向其原后继的指针就不存在了,再执行s->next = p->next时,相当于执行了 s->next=s,显然是错误的。本算法主要的时间开销在于查找第i-1个元素,时间复杂度为O(n)。若是在给定的结点后面插入新结点,则时间复杂度仅为O(1)。
扩展:对某一结点进行前插操作
前插操作是指在某结点的前面插入一个新结点,后插操作的定义刚好与之相反,在单链表插入算法中,通常都是釆用后插操作的。
以上面的算法为例,首先调用函数GetElem()找到第i-1个结点,即待插入结点的前驱结点后,再对其执行后插操作。由此可知,对结点的前插操作均可以转化为后插操作,前提是从单链表的头结点开始顺序查找到其前驱结点,时间复杂度为O(n)。
此外,可以釆用另一种方式将其转化为后插操作来实现,设待插入结点为*s,将插入到*p的前面。我们仍然将*s插入到*p的后面,然后将p->data与s->data交换即可,这样既满足了逻辑关系,又能使得时间复杂度为O(1)。算法的代码片段如下:
//将结点插入到*P之前的主要代码片段 s->next = p->next; //修改指针域,不能颠倒 p->next = s; temp = p->data; //交换数据域部分 p->data=s->data; s->data=temp;
删除结点操作
删除操作是将单链表的第i个结点删除。先检查删除位置的合法性,然后查找表中第i-1个结点,即被删结点的前驱结点,再将其删除。其操作过程如图2-7所示。
图2-7 单链表结点的删除
假设结点*p为找到的被删结点的前驱结点,为了实现这一操作后的逻辑关系的变化,仅需修改*p的指针域,即将*p的指针域next指向*q的下一结点。
实现删除结点的代码片段如下:
p=GetElem(L,i-1); //查找删除位置的前驱结点 q=p->next; //令q指向被删除结点 p->next=q->next //将*q结点从链中“断开” free (q) ; //释放结点的存储空间和插入算法一样,该算法的主要时间也是耗费在查找操作上,时间复杂度为O(n)。
扩展:删除结点*p
要实现删除某一个给定结点*p,通常的做法是先从链表的头结点开始顺序找到其前驱结点,然后再执行删除操作即可,算法的时间复杂度为O(n)。
其实,删除结点*p的操作可以用删除*p的后继结点操作来实现,实质就是将其后继结点的值赋予其自身,然后删除后继结点,也能使得时间复杂度为O(1)。
实现上述操作的代码片段如下:
q=p->next; //令q 向*p的后继结点 p->data=p->next->data; //和后继结点交换数据域 p->next=q->next; //将*q结点从链中“断开” free (q) ; //释放后继结点的存储空间
求表长操作
求表长操作就是计算单链表中数据结点(不含头结点)的个数,需要从第一个结点开始顺序依次访问表中的每一个结点,为此需要设置一个计数器变量,每访问一个结点,计数器加1,直到访问到空结点为止。算法的时间复杂度为O(n)。需要注意的是,因为单链表的长度是不包括头结点的,因此,不带头结点和带头结点的单链表在求表长操作上会略有不同。对不带头结点的单链表,当表为空时,要单独处理。
单链表是整个链表的基础,读者一定要熟练掌握单链表的基本操作算法,在设计算法时,建议先通过图示的方法理清算法的思路,然后再进行算法的编写。

