霍夫曼编码介绍
一种最古老而最优雅的数据压缩方法之一就是霍夫曼编码,它是一种基于最小冗余编码的压缩算法。最小冗余编码是指,如果知道一组数据中符号出现的频率,就可以用一种 特殊的方式来表示符号从而减少数据需要的存储空间。其方法是,使用较少的位对出现频率高的符号编码,用较多的位对出现频率低的符号编码。我们要意识到,一个符号不一定必须是文本字符,它可以是任何大小的数据,但往往它只占一个字节„
Sz = -lgPz
其中,Pz是数据集中z出现的概率,如果我们确切地知道z出现了多少次,那么Pz就是z出现的频率。来看一个例子,如果z在有32个符号的数据集中出现了8次,也就是1/4的概 率,那么z的熵为:
-lg(1/4) = 2位
这意味着,如果用超过两位的数来表示z将是一种浪费。如果在一般情况下用一个字节(即8位)来表示一个符号,那么在这种情况下使用压缩算法可以大幅减小数据的容量。
下表表示如何计算一个有72个数据实例(其中有5个不同的符号)熵的例子。要做到为 一点,将每个字符的熵相加。以“U”为例,字符的熵的计算方法如下。因为“U”出 现12次,所以毎个“U”的实例的熵计算如下:
-lg(12/72)=2.584 963位
由于“U”在数据中出现了12次,因此整个数据的熵为:
2.584 963 x 12=31.019 55位
为了计算数据的整体熵,将每个字符所贡献的熵相加。每个字符的熵在表中已经计算出来:
31.019 55+36.000 00+23.537 99+33.945 52+36.959 94=161.463 00位
如果使用8位来表示每个符号,需要72*8=576位的空间,所以理论上来说,可以最多将此数据压缩为:
1-(161.463 000/576)=72.0%
下图展示了用表格中的数据来构建一棵霍夫曼树的过程。构建的过程往往从叶子结点向上进行。首先,将毎个符号和频率放到它自身的树中(步骤1)。然后,将两个频率最小的根结点的树合并,并将其频率之和存放到树的新根结点中(步骤2)。这个过程反复持续下去,直到最后只剩下一棵树(这棵树就是霍夫曼 树,步骤5)。霍夫曼树的根结点包含数据中符号的总个数,它的叶子结点包含原始的符号和符号的频率。由于霍夫曼编码就是在不断寻找两棵最适合合并的树,因此它是贪婪算法的一个很好的例子。
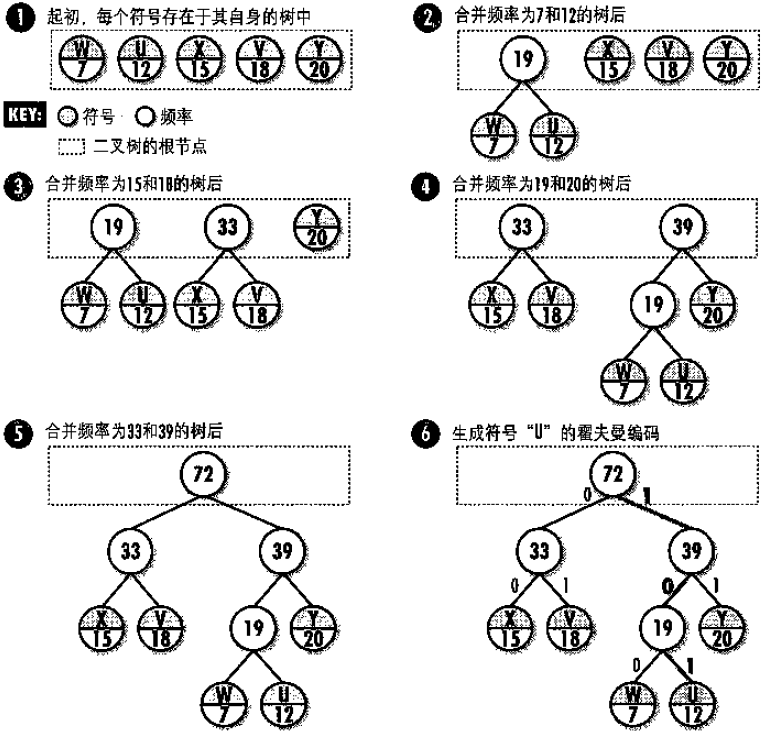
用表格中的数据构建霍夫曼树的过程
U=101, V=01, W=100, X=00, Y=11
要解压缩用霍夫曼树编码的数据,要一位一位地读取压缩数据。从树的根开始,当在数据中遇到0时,向树的左分支移动;当遇到1时,向右分支移动。一旦到达一个叶子结点,就找到了符号。接着从头开始,重复上述过程,直到所有的压缩数据都确定。用这种方法来解压缩数据是可能的,这是因为霍夫曼编码属于前缀树。前缀树是指一组代码中的任何一个编码都不是另一个编码的前缀。这就保证了编码被解码时不会有多义性。 例如,“V”的编码是01,01不会是任何其他编码的前缀。因此,只要在压缩数据中碰到了01,就可以确定它表示的是符号“V”。
12 * 3 + 18 * 2 + 7 * 3 + 15 * 2 + 20 * 2 = 163位
假设不使用压缩算法的72个字符均用8位来表示,那么其总共所占的数据大小为576位, 所以其压缩比计算如下:
1-(163/576)=71.7%
要再次强调的是,在实际中无法用小数位来表示霍夫曼编码,所以在很多情况下这个压缩比并没有数据的熵效果那么好。但它也非常接近于最佳压缩比。
在通常情况下,霍夫曼编码并不是最高效的压缩方法,但它压缩和解压缩的速度非常快。一般来说,造成霍夫曼编码比较耗时的原因是它需要扫描两次数据:一次用来计算频率,另一次才是用来压缩数据。而解压缩数据非常高效,因为解码每个符号的位序列只需要扫描一次霍夫曼树。
熵和最小冗余
首先,让我们重温在本章开始介绍的熵的概念,回想一下,毎个数据集都有一定的信息 量,这就是所谓的熵。一组数据的摘是数据中每个符号熵的总和.符号z的熵S定义为:Sz = -lgPz
其中,Pz是数据集中z出现的概率,如果我们确切地知道z出现了多少次,那么Pz就是z出现的频率。来看一个例子,如果z在有32个符号的数据集中出现了8次,也就是1/4的概 率,那么z的熵为:
-lg(1/4) = 2位
这意味着,如果用超过两位的数来表示z将是一种浪费。如果在一般情况下用一个字节(即8位)来表示一个符号,那么在这种情况下使用压缩算法可以大幅减小数据的容量。
下表表示如何计算一个有72个数据实例(其中有5个不同的符号)熵的例子。要做到为 一点,将每个字符的熵相加。以“U”为例,字符的熵的计算方法如下。因为“U”出 现12次,所以毎个“U”的实例的熵计算如下:
-lg(12/72)=2.584 963位
由于“U”在数据中出现了12次,因此整个数据的熵为:
2.584 963 x 12=31.019 55位
为了计算数据的整体熵,将每个字符所贡献的熵相加。每个字符的熵在表中已经计算出来:
31.019 55+36.000 00+23.537 99+33.945 52+36.959 94=161.463 00位
如果使用8位来表示每个符号,需要72*8=576位的空间,所以理论上来说,可以最多将此数据压缩为:
1-(161.463 000/576)=72.0%
| 符号 | 概率 | 每个实例的熵 | 总的熵 |
|---|---|---|---|
| U | 12/72 | 2.584 963 | 31.019 55 |
| V | 18/72 | 2.000 000 | 36.000 00 |
| W | 7/72 | 3.362 570 | 23.537 99 |
| X | 15/72 | 2.263 034 | 33.945 52 |
| Y | 20/72 | 1.847 997 | 36.959 94 |
构造霍夫曼树
霍夫曼编码展现了一种基于熵的数据近似的最佳表现形式。它首先生成一个称为霍夫曼 树的数据结构,霍夫曼树本身是一棵二叉树,用它来生成霍夫曼编码。霍夫曼编码是用来表示数据集合中符号的编码,用这种编码方式达到数据压缩的目的。然而,霍夫曼编码的压缩结果往往只能接近数据的熵,因为符号的熵常常是有小数位的,而在实际中,因为霍夫曼编码所用的位数不可能有小数位,所以有些代码会超过实际最优的代码位数。下图展示了用表格中的数据来构建一棵霍夫曼树的过程。构建的过程往往从叶子结点向上进行。首先,将毎个符号和频率放到它自身的树中(步骤1)。然后,将两个频率最小的根结点的树合并,并将其频率之和存放到树的新根结点中(步骤2)。这个过程反复持续下去,直到最后只剩下一棵树(这棵树就是霍夫曼 树,步骤5)。霍夫曼树的根结点包含数据中符号的总个数,它的叶子结点包含原始的符号和符号的频率。由于霍夫曼编码就是在不断寻找两棵最适合合并的树,因此它是贪婪算法的一个很好的例子。

用表格中的数据构建霍夫曼树的过程
压缩和解压缩数据
建立一棵霍夫曼数是数据压缩和解压缩的一部分。用霍夫曼树压縮数据,给定一个具体的符号,从树的根开始,然后沿着符号的叶向叶子结点追踪。在向下追踪的过程中,当向左分支移动时,向当前编码末尾追加0,当向右移动时,向当前编码末尾追加 1。所以,在图中为了确定“U”的霍曼夫编码,首先向右移动(1),然后向左(10),然后再向右(101)。图中符号的霍夫曼编码为:U=101, V=01, W=100, X=00, Y=11
要解压缩用霍夫曼树编码的数据,要一位一位地读取压缩数据。从树的根开始,当在数据中遇到0时,向树的左分支移动;当遇到1时,向右分支移动。一旦到达一个叶子结点,就找到了符号。接着从头开始,重复上述过程,直到所有的压缩数据都确定。用这种方法来解压缩数据是可能的,这是因为霍夫曼编码属于前缀树。前缀树是指一组代码中的任何一个编码都不是另一个编码的前缀。这就保证了编码被解码时不会有多义性。 例如,“V”的编码是01,01不会是任何其他编码的前缀。因此,只要在压缩数据中碰到了01,就可以确定它表示的是符号“V”。
霍夫曼编码的效率
为了确定霍夫曼编码降低了多大容量的存储空间,首先要计算毎个符号的频率与其编码位数的乘积,然后将其求和。所以,图中和表中压缩后的数据的大小为:12 * 3 + 18 * 2 + 7 * 3 + 15 * 2 + 20 * 2 = 163位
假设不使用压缩算法的72个字符均用8位来表示,那么其总共所占的数据大小为576位, 所以其压缩比计算如下:
1-(163/576)=71.7%
要再次强调的是,在实际中无法用小数位来表示霍夫曼编码,所以在很多情况下这个压缩比并没有数据的熵效果那么好。但它也非常接近于最佳压缩比。
在通常情况下,霍夫曼编码并不是最高效的压缩方法,但它压缩和解压缩的速度非常快。一般来说,造成霍夫曼编码比较耗时的原因是它需要扫描两次数据:一次用来计算频率,另一次才是用来压缩数据。而解压缩数据非常高效,因为解码每个符号的位序列只需要扫描一次霍夫曼树。

