C语言要发就发(1898)问题

问题描述

“1898—要发就发”。请将不超过1993的所有素数从小到大排成第一行，第二行上的每个数都等于它上面相邻两个素数之差。编程求出：第二行数中是否存在若干个连续的整数，它们的和恰好为1898？假如存在的话，又有几种这样的情况？

两行数据分别如下：
第一行：2  3  5  7  11  13  17......1979  1987  1993
第二行：1  2  2  4   2   4......8  6

问题分析

从数学上对该问题进行分析如下。

假设第一行中的素数为n[l]、n[2]、n[3]-n[i]、…，而第二行中的差值为m[1]、m[2]、…。则m[j]可以表示为：

m[j]=n[j+1]-n[j]

第二行中连续N个数的和sum可以表示为：

sum=m[k]+m[k+1]+m[k+2]+m[k+3]+...+m[j]
       =(n[k+1]-n[k])+(n[k+2]-n[k+1])+(n[k+3]-n[k+2])+...+(n[j+1]-n[j])
       = n[k+1]-n[k]+n[k+2]-n[k+1]+n[k+3]-n[k+2]+...+n[j+1]-n[j]
       =n[j+1]-n[k]

其中j>k≥1。

因此，原题目可以转换成这样的等价问题：在不超过1993的所有素数中是否存在这样两个素数，它们的差恰好是1898。若存在，则第二行中必有所需整数序列，且其和恰为1898。

显然，对原问题的等价问题的求解是比较简单的。

在求解等价问题时，第一行的素数序列可以从3开始考虑，因为任意的素数与2的差一定为奇数，不可能为1898，所以在求解时素数序列中不需要包含2。

算法设计

首先釆用数组number[NUM]来存放第一行中的全部素数，由前面分析可知，从3开始存放即可，一直到1993。

在产生不超过1993的素数序列时可以采用函数来判断一个整数是否为素数。如果是素数，则将其存放到数组中，否则不需存放。

定义一个函数，函数名设为fun，在其中判断传进来的形参是否为素数，如果是素数则返回1，否则返回0。需要注意的是，在所有偶数中，只有2是唯一的素数。在函数fun()中，可以分为以下5种情况来判断：

• n<1，由题意可知，本题不考虑素数为1的情况，且n<l时显然不是素数，所以返回0。
• n=2,是素数，返回1。
• n是偶数，不是素数，返回0。
• n是奇数，不是素数，返回0。
• n≠2是素数，返回1。

在主函数中，使用循环结构。

从第一行中最大的素数开始搜索，用它逐个减去number[0]、number[1]、......每减一次判断一次，看它们的差值是否大于1989。直到在数组number[NUM]中找到一个位置j，使得最大素数与number[j]的差值不大于1989。此时，需要判断它们的差值是否等于1989，如果恰好等于1989，则最大素数与number[j]中存放的素数就是我们找到第一个结果集。

对第一行中次大的素数重复该搜索过程，依次类推，直到第一行中大于1989且与1989最接近的那个素数为止。

程序流程图：


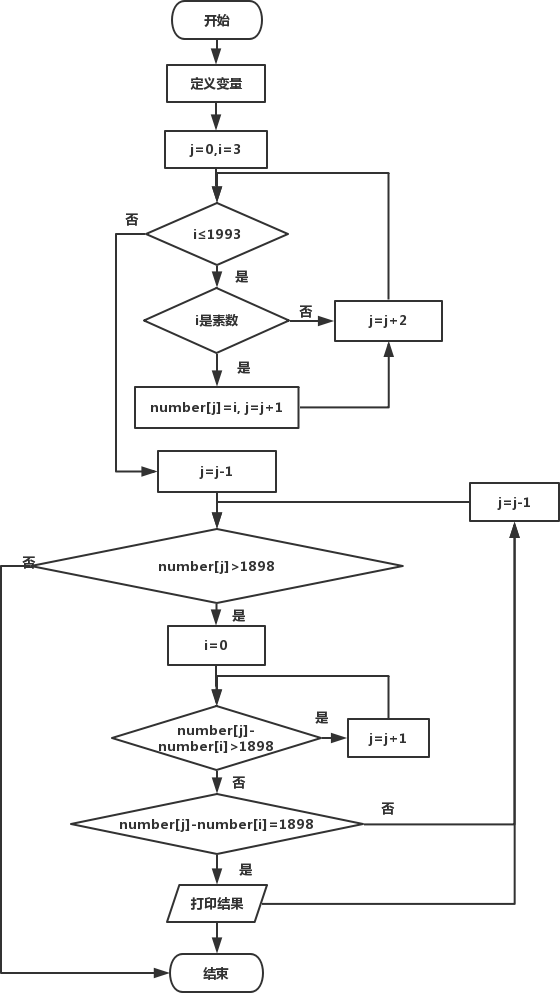
下面是完整的代码：

#include<stdio.h>
#include<math.h>

#define NUM 320

int number[NUM];  /*存放不超过1993的全部素数*/
int fun(int i);

int main()
{
    int i, j, count=0;
    printf("列出第一行中差值为1989的所有素数组合:\n");
    for(j=0, i=3; i<=1993; i+=2)  /*求出不超过1993的全部素数*/
        if( fun(i) )
            number[j++]=i;
    for(j--; number[j]>1898; j--)  /*从最大的素数开始向1898搜索*/
    {
        for(i=0; number[j]-number[i]>1898; i++);  /*循环查找满足条件的素数*/
        if(number[j]-number[i] == 1898)  /*若两个素数的差为1898，则输出*/
            printf("(%d).%3d,%d\n", ++count, number[i], number[j]);
    }
   
    return 0;
}

int fun(int i)
{
    int j;
    if( i<=1 )
        return 0;  /*判断是否为素数，为1是素数，为0不是素数*/
    if( i==2 )
        return 1;
    if( !(i%2) )
        return 0;  /*if no, return 0*/
    for(j=3; j<=(int)(sqrt((double)i)+1); j+=2)
        if( !(i%j) ) return 0;
    return 1;
}

运行结果：
列出第一行中差值为1989的所有素数组合:
(1). 89,1987
(2). 53,1951
(3).  3,1901