2.2线性表的顺序存储及运算—顺序表应用举例
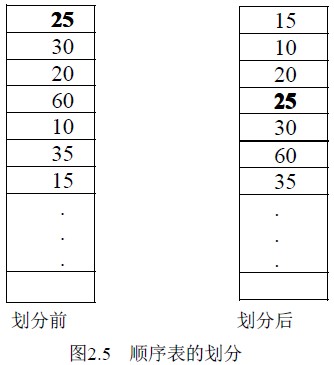
例2．1 将顺序表(a1，a2，... ，an) 重新排列为以a1 为界的两部分：a1 前面的值均比a1 小，a1 后面的值都比a1 大(这里假设数据元素的类型具有可比性, 不妨设为整型)，操作前后如图2.5所示。这一操作称为划分。a1 也称为基准。
划分的方法有多种，下面介绍的划分算法其思路简单，性能较差。基本思路：
从第二个元素开始到最后一个元素，逐一向后扫描：
（1）当前数据元素aI 比a1 大时，表明它已经在a1 的后面，不必改变它与a1 之间的位置，继续比较下一个。
（2）当前结点若比a1 小，说明它应该在a1 的前面，此时将它上面的元素都依次向下移动一个位置，然后将它置入最上方。
算法如下：
void part(SeqList *L)
{ int i,j;
datatype x,y;
x=L->data[0]; /* 将基准置入x 中*/
for(i=1;i<=L->last;i++)
if(L->data[i]<x) /*当前元素小于基准*/
{ y = L->data[i];
for(j=i-1;j>=0;j--) /*移动*/
L－>data[j+1]=L->data[j];
L->data[0]=y;
}
}
算法2.5
本算法中，有两重循环，外循环执行n－1次，内循环中移动元素的次数与当前数据的大小有关，当第ｉ个元素小于a1 时，要移动它上面的i-1个元素，再加上当前结点的保存及置入，所以移动i-1+2次，在最坏情况下，a1 后面的结点都小于a1 ，故总的移动次数为：
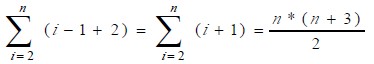即最坏情况下移动数据时间性能为Ｏ(ｎ２)。
这个算法简单但效率低，在第９章的快速排序中时我们将介绍另一种划分算法，它的性能为Ｏ(n)。
例2．2 有顺序表A和B，其元素均按从小到大的升序排列，编写一个算法将它们合并成一个顺序表C，要求C的元素也是从小到大的升序排列。
算法思路：依次扫描通过A和B的元素，比较当前的元素的值，将较小值的元素赋给C，如此直到一个线性表扫描完毕，然后将未完的那个顺序表中余下部分赋给C即可。C的容量要能够容纳A、B两个线性表相加的长度。
算法如下：
void merge(SeqList A, SeqList B, SeqList *C)
{ int i,j,k;
i=0;j=0;k=0;
while ( i<=A.last && j<=B.last )
if (A.date[i]<B.date[j])
C->data[k++]=A.data[i++];
else C->data[k++]=B.data[j++];
while (i<=A.last )
C->data[k++]= A.data[i++];
while (j<=B.last )
C->data[k++]=B.data[j++];
C->last=k-1;
}
算法2.6
算法的时间性能是O(m+n)，其中m是A的表长，n是B的表长。
例2.3 比较两个线性表的大小。两个线性表的比较依据下列方法：设A、B是两个线性表，均用向量表示，表长分别为m和n。A′和B′分别为A 和B 中除去最大共同前缀后的子表。
例如A=(x,y,y,z,x,z)， B=(x,y,y,z,y,x,x,z)，两表最大共同前缀为(x,y,y,z) 。则A′=（x,z）， B′=（y,x,x,z），若A′=B′= 空表，则A=B；若A′=空表且B′≠空表，或两者均不空且A′首元素小于B′首元素，则A<B；否则，A>B。
算法思路：首先找出A、B的最大共同前缀；然后求出A′和B′，之后在按比较规则进行比较，A>B 函数返回1；A=B返回0；A<B返回-1。算法如下：
int compare( A,B,m,n)
int A[],B[];
int m,n;
{ int i=0,j,AS[],BS[],ms=0,ns=0; /*AS,BS作为A′,B′*/
while (A[i]==B[i]) i++; /*找最大共同前缀*/
for (j=i;j<m;j++)
{ AS[j-i]=A[j];ms++; } /*求A′,ms为A′的长度*/
for (j=i;j<n;j++)
{ BS[j-i]=B[j];ns++; } /*求B′,ms为B′的长度*/
if (ms==ns&&ms==0) return 0;
else if (ms==0&&ns>0 || ms>0 && ns>0 && AS[0]<BS[0]) return –1;
else return 1;
}
算法2.7
算法的时间性能是O( m+n )。
划分的方法有多种，下面介绍的划分算法其思路简单，性能较差。基本思路：
从第二个元素开始到最后一个元素，逐一向后扫描：
（1）当前数据元素aI 比a1 大时，表明它已经在a1 的后面，不必改变它与a1 之间的位置，继续比较下一个。
（2）当前结点若比a1 小，说明它应该在a1 的前面，此时将它上面的元素都依次向下移动一个位置，然后将它置入最上方。
算法如下：
void part(SeqList *L)
{ int i,j;
datatype x,y;
x=L->data[0]; /* 将基准置入x 中*/
for(i=1;i<=L->last;i++)
if(L->data[i]<x) /*当前元素小于基准*/
{ y = L->data[i];
for(j=i-1;j>=0;j--) /*移动*/
L－>data[j+1]=L->data[j];
L->data[0]=y;
}
}
算法2.5
本算法中，有两重循环，外循环执行n－1次，内循环中移动元素的次数与当前数据的大小有关，当第ｉ个元素小于a1 时，要移动它上面的i-1个元素，再加上当前结点的保存及置入，所以移动i-1+2次，在最坏情况下，a1 后面的结点都小于a1 ，故总的移动次数为：
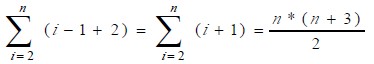
这个算法简单但效率低，在第９章的快速排序中时我们将介绍另一种划分算法，它的性能为Ｏ(n)。
例2．2 有顺序表A和B，其元素均按从小到大的升序排列，编写一个算法将它们合并成一个顺序表C，要求C的元素也是从小到大的升序排列。
算法思路：依次扫描通过A和B的元素，比较当前的元素的值，将较小值的元素赋给C，如此直到一个线性表扫描完毕，然后将未完的那个顺序表中余下部分赋给C即可。C的容量要能够容纳A、B两个线性表相加的长度。
算法如下：
void merge(SeqList A, SeqList B, SeqList *C)
{ int i,j,k;
i=0;j=0;k=0;
while ( i<=A.last && j<=B.last )
if (A.date[i]<B.date[j])
C->data[k++]=A.data[i++];
else C->data[k++]=B.data[j++];
while (i<=A.last )
C->data[k++]= A.data[i++];
while (j<=B.last )
C->data[k++]=B.data[j++];
C->last=k-1;
}
算法2.6
算法的时间性能是O(m+n)，其中m是A的表长，n是B的表长。
例2.3 比较两个线性表的大小。两个线性表的比较依据下列方法：设A、B是两个线性表，均用向量表示，表长分别为m和n。A′和B′分别为A 和B 中除去最大共同前缀后的子表。
例如A=(x,y,y,z,x,z)， B=(x,y,y,z,y,x,x,z)，两表最大共同前缀为(x,y,y,z) 。则A′=（x,z）， B′=（y,x,x,z），若A′=B′= 空表，则A=B；若A′=空表且B′≠空表，或两者均不空且A′首元素小于B′首元素，则A<B；否则，A>B。
算法思路：首先找出A、B的最大共同前缀；然后求出A′和B′，之后在按比较规则进行比较，A>B 函数返回1；A=B返回0；A<B返回-1。算法如下：
int compare( A,B,m,n)
int A[],B[];
int m,n;
{ int i=0,j,AS[],BS[],ms=0,ns=0; /*AS,BS作为A′,B′*/
while (A[i]==B[i]) i++; /*找最大共同前缀*/
for (j=i;j<m;j++)
{ AS[j-i]=A[j];ms++; } /*求A′,ms为A′的长度*/
for (j=i;j<n;j++)
{ BS[j-i]=B[j];ns++; } /*求B′,ms为B′的长度*/
if (ms==ns&&ms==0) return 0;
else if (ms==0&&ns>0 || ms>0 && ns>0 && AS[0]<BS[0]) return –1;
else return 1;
}
算法2.7
算法的时间性能是O( m+n )。
