2.3线性表的链式存储和运算—双向链表
以上讨论的单链表的结点中只有一个指向其后继结点的指针域next,因此若已知某结点的指针为p,其后继结点的指针则为p->next ,而找其前驱则只能从该链表的头指针开始,顺着各结点的next 域进行,也就是说找后继的时间性能是O(1),找前驱的时间性能是O(n),如果也希望找前驱的时间性能达到O(1),则只能付出空间的代价:每个结点再加一个指向前驱的指针域,结点的结构为如图2.18 所示,用这种结点组成的链表称为双向链表。
 双向链表结点的定义如下:
双向链表结点的定义如下:
typedef struct dlnode
{ datatype data;
struct dlnode *prior,*next;
}DLNode,*DLinkList;
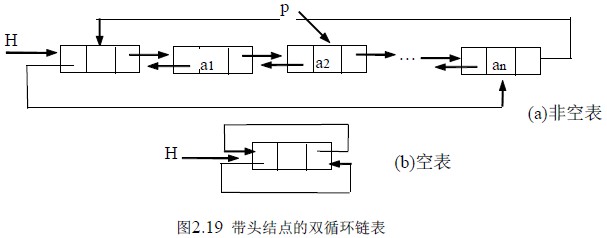
和单链表类似,双向链表通常也是用头指针标识,也可以带头结点和做成循环结构,图2.19 是带头结点的双向循环链表示意图。显然通过某结点的指针p 即可以直接得到它的后继结点的指针p->next,也可以直接得到它的前驱结点的的指针p->prior。这样在有些操作中需要找前驱时,则勿需再用循环。从下面的插入删除运算中可以看到这一点。
设p 指向双向循环链表中的某一结点,即p 中是该结点的指针,则p->prior->next 表示的是*p 结点之前驱结点的后继结点的指针,即与p 相等;类似,p->next->prior 表示的是*p 结点之后继结点的前驱结点的指针,也与p 相等,所以有以下等式:
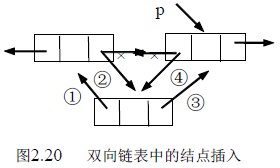
双向链表中结点的插入:设p 指向双向链表中某结点,s 指向待插入的值为x 的新结点,将*s 插入到*p 的前面,插入示意图如图2.20 所示。操作如下:
1 s->prior=p->prior;
2 p->prior->next=s;
3 s->next=p;
4 p->prior=s;
指针操作的顺序不是唯一的,但也不是任意的,操作①必须要放到操作④的前面完成,否则*p的前驱结点的指针就丢掉了。读者把每条指针操作的涵义搞清楚,就不难理解了。
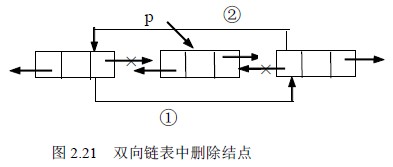
双向链表中结点的删除:
设p 指向双向链表中某结点,删除*p。
操作示意图如图2.21 所示。操作如下:
①p->prior->next=p->next;
②p->next->prior=p->prior;
free(p);

typedef struct dlnode
{ datatype data;
struct dlnode *prior,*next;
}DLNode,*DLinkList;
和单链表类似,双向链表通常也是用头指针标识,也可以带头结点和做成循环结构,图2.19 是带头结点的双向循环链表示意图。显然通过某结点的指针p 即可以直接得到它的后继结点的指针p->next,也可以直接得到它的前驱结点的的指针p->prior。这样在有些操作中需要找前驱时,则勿需再用循环。从下面的插入删除运算中可以看到这一点。
设p 指向双向循环链表中的某一结点,即p 中是该结点的指针,则p->prior->next 表示的是*p 结点之前驱结点的后继结点的指针,即与p 相等;类似,p->next->prior 表示的是*p 结点之后继结点的前驱结点的指针,也与p 相等,所以有以下等式:
p->prior->next = p = p->next->prior

双向链表中结点的插入:设p 指向双向链表中某结点,s 指向待插入的值为x 的新结点,将*s 插入到*p 的前面,插入示意图如图2.20 所示。操作如下:
1 s->prior=p->prior;
2 p->prior->next=s;
3 s->next=p;
4 p->prior=s;
指针操作的顺序不是唯一的,但也不是任意的,操作①必须要放到操作④的前面完成,否则*p的前驱结点的指针就丢掉了。读者把每条指针操作的涵义搞清楚,就不难理解了。
双向链表中结点的删除:
设p 指向双向链表中某结点,删除*p。
操作示意图如图2.21 所示。操作如下:
①p->prior->next=p->next;
②p->next->prior=p->prior;
free(p);



