3.1 栈—栈的存储实现和运算实现
由于栈是运算受限的线性表,因此线性表的存储结构对栈也是适用的,只是操作不同而已。
利用顺序存储方式实现的栈称为顺序栈。类似于顺序表的定义,栈中的数据元素用一个预设的足够长度的一维数组来实现:datatype data[MAXSIZE],栈底位置可以设置在数组的任一个端点,而栈顶是随着插入和删除而变化的,用一个int top 来作为栈顶的指针,指明当前栈顶的位置,同样将data 和top 封装在一个结构中,顺序栈的类型描述如下:
#define MAXSIZE 1024
typedef struct
{datatype data[MAXSIZE];
int top;
}SeqStack
定义一个指向顺序栈的指针:
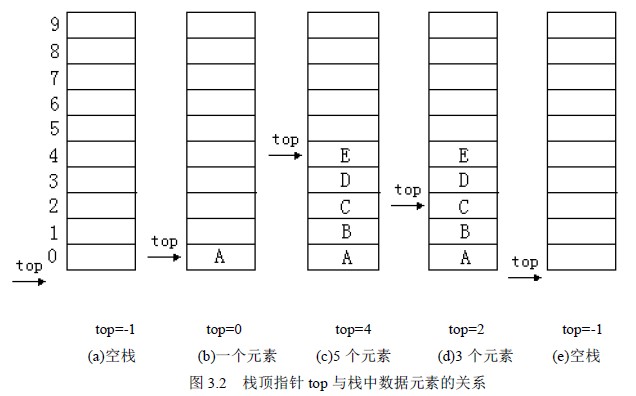
图(a)是空栈,图(c)是A、B、C、D、E 5 个元素依次入栈之后,图(d)是在图(c)之后E、D 相继出栈,此时栈中还有3 个元素,或许最近出栈的元素D、E 仍然在原先的单元存储着,但top 指针已经指向了新的栈顶,则元素D、E 已不在栈中了,通过这个示意图要深刻理解栈顶指针的作用。
在上述存储结构上基本操作的实现如下:
⑴ 置空栈:首先建立栈空间,然后初始化栈顶指针。
SeqStack *Init_SeqStack()
{ SeqStack *s;
s=malloc(sizeof(SeqStack));
s->top= -1; return s;
}
⑵ 判空栈
int Empty_SeqStack(SeqStack *s)
{ if (s->top= = -1) return 1;
else return 0;
}
⑶ 入栈
int Push_SeqStack (SeqStack *s, datatype x)
{if (s->top= =MAXSIZE-1) return 0; /*栈满不能入栈*/
else { s->top++;
s->data[s->top]=x;
return 1;
}
}
⑷ 出栈
int Pop_SeqStack(SeqStack *s, datatype *x)
{ if (Empty_SeqStack ( s ) ) return 0; /*栈空不能出栈*/
else { *x=s->data[s->top];
s->top--; return 1; } /*栈顶元素存入*x,返回*/
}
⑸ 取栈顶元素
datatype Top_SeqStack(SeqStack *s)
{ if ( Empty_SeqStack ( s ) ) return 0; /*栈空*/
else return (s->data[s->top] );
}
以下几点说明:
1. 对于顺序栈,入栈时,首先判栈是否满了,栈满的条件为:s->top= =MAXSIZE-1,栈满时,不能入栈; 否则出现空间溢出,引起错误,这种现象称为上溢。
2. 出栈和读栈顶元素操作,先判栈是否为空,为空时不能操作,否则产生错误。通常栈空时常作为一种控制转移的条件。
用链式存储结构实现的栈称为链栈。通常链栈用单链表表示,因此其结点结构与单链表的结构相同,在此用LinkStack 表示,即有:
typedef struct node
{ datatype data;
struct node *next;
}StackNode,* LinkStack;
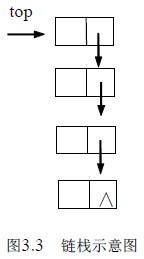
说明top 为栈顶指针: LinkStack top ;因为栈中的主要运算是在栈顶插入、删除,显然在链表的头部做栈顶是最方便的,而且没有必要象单链表那样为了运算方便附加一个头结点。通常将链栈表示成图3.3 的形式。
链栈基本操作的实现如下:
⑴ 置空栈
LinkStack Init_LinkStack()
{ return NULL;
}
⑵ 判栈空
int Empty_LinkStack(LinkStack top )
{ if(top==-1) return 1;
else return 0;
}
⑶ 入栈
LinkStack Push_LinkStack(LinkStack top, datatype x)
{ StackNode *s;
s=malloc(sizeof(StackNode));
s->data=x;
s->next=top;
top=s;
return top;
}
⑷ 出栈
LinkStack Pop_LinkStack (LinkStack top, datatype *x)
{ StackNode *p;
if (top= =NULL) return NULL;
else { *x = top->data;
p = top;
top = top->next;
free (p);
return top;
}
}
1. 顺序栈
利用顺序存储方式实现的栈称为顺序栈。类似于顺序表的定义,栈中的数据元素用一个预设的足够长度的一维数组来实现:datatype data[MAXSIZE],栈底位置可以设置在数组的任一个端点,而栈顶是随着插入和删除而变化的,用一个int top 来作为栈顶的指针,指明当前栈顶的位置,同样将data 和top 封装在一个结构中,顺序栈的类型描述如下:
#define MAXSIZE 1024
typedef struct
{datatype data[MAXSIZE];
int top;
}SeqStack
定义一个指向顺序栈的指针:
SeqStack *s;
通常0 下标端设为栈底,这样空栈时栈顶指针top=-1; 入栈时,栈顶指针加1,即s->top++; 出栈时,栈顶指针减1,即s->top--。栈操作的示意图如图3.2 所示。图(a)是空栈,图(c)是A、B、C、D、E 5 个元素依次入栈之后,图(d)是在图(c)之后E、D 相继出栈,此时栈中还有3 个元素,或许最近出栈的元素D、E 仍然在原先的单元存储着,但top 指针已经指向了新的栈顶,则元素D、E 已不在栈中了,通过这个示意图要深刻理解栈顶指针的作用。
在上述存储结构上基本操作的实现如下:

⑴ 置空栈:首先建立栈空间,然后初始化栈顶指针。
SeqStack *Init_SeqStack()
{ SeqStack *s;
s=malloc(sizeof(SeqStack));
s->top= -1; return s;
}
⑵ 判空栈
int Empty_SeqStack(SeqStack *s)
{ if (s->top= = -1) return 1;
else return 0;
}
⑶ 入栈
int Push_SeqStack (SeqStack *s, datatype x)
{if (s->top= =MAXSIZE-1) return 0; /*栈满不能入栈*/
else { s->top++;
s->data[s->top]=x;
return 1;
}
}
⑷ 出栈
int Pop_SeqStack(SeqStack *s, datatype *x)
{ if (Empty_SeqStack ( s ) ) return 0; /*栈空不能出栈*/
else { *x=s->data[s->top];
s->top--; return 1; } /*栈顶元素存入*x,返回*/
}
⑸ 取栈顶元素
datatype Top_SeqStack(SeqStack *s)
{ if ( Empty_SeqStack ( s ) ) return 0; /*栈空*/
else return (s->data[s->top] );
}
以下几点说明:
1. 对于顺序栈,入栈时,首先判栈是否满了,栈满的条件为:s->top= =MAXSIZE-1,栈满时,不能入栈; 否则出现空间溢出,引起错误,这种现象称为上溢。
2. 出栈和读栈顶元素操作,先判栈是否为空,为空时不能操作,否则产生错误。通常栈空时常作为一种控制转移的条件。
2. 链栈
用链式存储结构实现的栈称为链栈。通常链栈用单链表表示,因此其结点结构与单链表的结构相同,在此用LinkStack 表示,即有:
typedef struct node
{ datatype data;
struct node *next;
}StackNode,* LinkStack;
说明top 为栈顶指针: LinkStack top ;因为栈中的主要运算是在栈顶插入、删除,显然在链表的头部做栈顶是最方便的,而且没有必要象单链表那样为了运算方便附加一个头结点。通常将链栈表示成图3.3 的形式。
链栈基本操作的实现如下:
⑴ 置空栈
LinkStack Init_LinkStack()
{ return NULL;
}
⑵ 判栈空
int Empty_LinkStack(LinkStack top )

{ if(top==-1) return 1;
else return 0;
}
⑶ 入栈
LinkStack Push_LinkStack(LinkStack top, datatype x)
{ StackNode *s;
s=malloc(sizeof(StackNode));
s->data=x;
s->next=top;
top=s;
return top;
}
⑷ 出栈
LinkStack Pop_LinkStack (LinkStack top, datatype *x)
{ StackNode *p;
if (top= =NULL) return NULL;
else { *x = top->data;
p = top;
top = top->next;
free (p);
return top;
}
}

