3.4 队列应用举例
例3.5 求迷宫的最短路径:
现要求设计一个算法找一条从迷宫入口到出口的最短路径。本算法要求找一条迷宫的最短路径,算法的基本思想为:从迷宫入口点(1,1)出发,向四周搜索,记下所有一步能到达的坐标点;然后依次再从这些点出发,再记下所有一步能到达的坐标点,…,依此类推,直到到达迷宫的出口点(m,n)为止,然后从出口点沿搜索路径回溯直至入口。这样就找到了一条迷宫的最短路径,否则迷宫无路径。
有关迷宫的数据结构、试探方向、如何防止重复到达某点以避免发生死循环的问题与例3.2 处理相同,不同的是:如何存储搜索路径。在搜索过程中必须记下每一个可到达的坐标点,以便从这些点出发继续向四周搜索。由于先到达的点先向下搜索,故引进一个“先进先出”数据结构------队列来保存已到达的坐标点。到达迷宫的出口点(m,n)后,为了能够从出口点沿搜索路径回溯直至入口,对于每一点,记下坐标点的同时,还要记下到达该点的前驱点,因此,用一个结构数组sq[num]作为队列的存储空间,因为迷宫中每个点至多被访问一次,所以num 至多等于m*n。sq 的每一个结构有三个域:x,y 和pre,其中x,y 分别为所到达的点的坐标,pre 为前驱点在sq 中的坐标,是一个静态链域。除sq 外,还有队头、队尾指针:front 和rear 用来指向队头和队尾元素。
队的定义如下:
typedef struct
{ int x,y;
int pre;
}sqtype;
sqtype sq[num];
int front,rear;
初始状态,队列中只有一个元素sq[1]记录的是入口点的坐标(1,1),因为该点是出发点,因此没有前驱点,pre 域为-1,队头指针front 和队尾指针rear 均指向它,此后搜索时都是以front 所指点为搜索的出发点,当搜索到一个可到达点时,即将该点的坐标及front 所指点的位置入队,不但记下了到达点的坐标,还记下了它的前驱点。front 所指点的8个方向搜索完毕后,则出队,继续对下一点搜索。搜索过程中遇到出口点则成功,搜索结束,打印出迷宫最短路径,算法结束;或者当前队空即没有搜索点了,表明没有路径算法也结束。
算法如下:
void path(maze,move)
int maze[m][n];/*迷宫数组*/
item move[8];/*坐标增量数组*/
{ sqtype sq[NUM];
int front,rear;
int x,y,i,j,v;
front=rear=0;
sq[0].x=1; sq[0].y=1; sq[0].pre=-1; /*入口点入队*/
maze[1,1]=-1;
while (front<=rear) /*队列不空*/
{ x=sq[front].x ; y=sq[front ].y ;
for (v=0;v<8;v++)
{ i=x+move[v].x; j=x+move[v].y;
if (maze[i][j]==0)
{ rear++;
sq[rear].x=i; sq[rear].y=j; sq[rear].pre=front;
maze[i][j]=-1;
}
if (i==m&&j==n)
{ printpath(sq,rear); /*打印迷宫*/
restore(maze); /*恢复迷宫*/
return 1;
}
} /*for v*/
front++; /*当前点搜索完,取下一个点搜索*/
} /*while*/
return 0;
} /*path*/
void printpath(sqtype sq[],int rear) /*打印迷宫路径*/
{ int i;
i=rear;
do { printf(" (%d,%d)",sq[i].x , sq[i].y) ;
i=sq[i].pre; /*回溯*/
} while (i!=-1);
} /*printpath*/
算法3.5
对于图3.17(a)所示的迷宫搜索过程如图和队列中的数据如图3.17(a)、(b)所示。
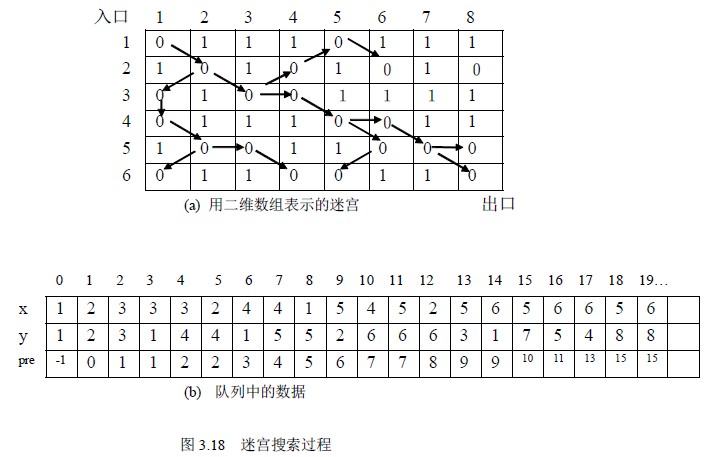
运行结果: (6,8) (5,7) (4,6)(4,5) (3,4) (3,3) (2,2)(1,1)
在上面的例子中,不能采用循环队列,因为在本问题中,队列中保存了探索到的路径序列,如果用循环队列,则把先前得到的路径序列覆盖掉。而在有些问题中,如持续运行的实时监控系统中,监控系统源源不断的收到监控对象顺序发来的信息如报警,为了保持报警信息的顺序性,就要按顺序一一保存,而这些信息是无穷多个,不可能全部同时驻留内存,可根据实际问题,设计一个适当大的向量空间,用作循环队列,最初收到的报警信息一一入队,当队满之后,又有新的报警到来到时,新的报警则覆盖掉了旧的报警,内存中始终保持当前最新的若干条报警,以便满足快速查询。
现要求设计一个算法找一条从迷宫入口到出口的最短路径。本算法要求找一条迷宫的最短路径,算法的基本思想为:从迷宫入口点(1,1)出发,向四周搜索,记下所有一步能到达的坐标点;然后依次再从这些点出发,再记下所有一步能到达的坐标点,…,依此类推,直到到达迷宫的出口点(m,n)为止,然后从出口点沿搜索路径回溯直至入口。这样就找到了一条迷宫的最短路径,否则迷宫无路径。
有关迷宫的数据结构、试探方向、如何防止重复到达某点以避免发生死循环的问题与例3.2 处理相同,不同的是:如何存储搜索路径。在搜索过程中必须记下每一个可到达的坐标点,以便从这些点出发继续向四周搜索。由于先到达的点先向下搜索,故引进一个“先进先出”数据结构------队列来保存已到达的坐标点。到达迷宫的出口点(m,n)后,为了能够从出口点沿搜索路径回溯直至入口,对于每一点,记下坐标点的同时,还要记下到达该点的前驱点,因此,用一个结构数组sq[num]作为队列的存储空间,因为迷宫中每个点至多被访问一次,所以num 至多等于m*n。sq 的每一个结构有三个域:x,y 和pre,其中x,y 分别为所到达的点的坐标,pre 为前驱点在sq 中的坐标,是一个静态链域。除sq 外,还有队头、队尾指针:front 和rear 用来指向队头和队尾元素。
队的定义如下:
typedef struct
{ int x,y;
int pre;
}sqtype;
sqtype sq[num];
int front,rear;
初始状态,队列中只有一个元素sq[1]记录的是入口点的坐标(1,1),因为该点是出发点,因此没有前驱点,pre 域为-1,队头指针front 和队尾指针rear 均指向它,此后搜索时都是以front 所指点为搜索的出发点,当搜索到一个可到达点时,即将该点的坐标及front 所指点的位置入队,不但记下了到达点的坐标,还记下了它的前驱点。front 所指点的8个方向搜索完毕后,则出队,继续对下一点搜索。搜索过程中遇到出口点则成功,搜索结束,打印出迷宫最短路径,算法结束;或者当前队空即没有搜索点了,表明没有路径算法也结束。
算法如下:
void path(maze,move)
int maze[m][n];/*迷宫数组*/
item move[8];/*坐标增量数组*/
{ sqtype sq[NUM];
int front,rear;
int x,y,i,j,v;
front=rear=0;
sq[0].x=1; sq[0].y=1; sq[0].pre=-1; /*入口点入队*/
maze[1,1]=-1;
while (front<=rear) /*队列不空*/
{ x=sq[front].x ; y=sq[front ].y ;
for (v=0;v<8;v++)
{ i=x+move[v].x; j=x+move[v].y;
if (maze[i][j]==0)
{ rear++;
sq[rear].x=i; sq[rear].y=j; sq[rear].pre=front;
maze[i][j]=-1;
}
if (i==m&&j==n)
{ printpath(sq,rear); /*打印迷宫*/
restore(maze); /*恢复迷宫*/
return 1;
}
} /*for v*/
front++; /*当前点搜索完,取下一个点搜索*/
} /*while*/
return 0;
} /*path*/
void printpath(sqtype sq[],int rear) /*打印迷宫路径*/
{ int i;
i=rear;
do { printf(" (%d,%d)",sq[i].x , sq[i].y) ;
i=sq[i].pre; /*回溯*/
} while (i!=-1);
} /*printpath*/
算法3.5
对于图3.17(a)所示的迷宫搜索过程如图和队列中的数据如图3.17(a)、(b)所示。

运行结果: (6,8) (5,7) (4,6)(4,5) (3,4) (3,3) (2,2)(1,1)
在上面的例子中,不能采用循环队列,因为在本问题中,队列中保存了探索到的路径序列,如果用循环队列,则把先前得到的路径序列覆盖掉。而在有些问题中,如持续运行的实时监控系统中,监控系统源源不断的收到监控对象顺序发来的信息如报警,为了保持报警信息的顺序性,就要按顺序一一保存,而这些信息是无穷多个,不可能全部同时驻留内存,可根据实际问题,设计一个适当大的向量空间,用作循环队列,最初收到的报警信息一一入队,当队满之后,又有新的报警到来到时,新的报警则覆盖掉了旧的报警,内存中始终保持当前最新的若干条报警,以便满足快速查询。

