4.2 串的定长顺序存储及基本运算
因为串是数据元素类型为字符型的线性表,所以线性表的存储方式仍适用于串,也因为字符的特殊性和字符串经常作为一个整体来处理的特点,串在存储时还有一些与一般线性表不同之处。
类似于顺序表,用一组地址连续的存储单元存储串值中的字符序列,所谓定长是指按预定义的大小,为每一个串变量分配一个固定长度的存储区,如:
#define MAXSIZE 256
char s[MAXSIZE];
则串的最大长度不能超过256。
如何标识实际长度?
1. 类似顺序表,用一个指针来指向最后一个字符,这样表示的串描述如下:
typedef struct
{ char data[MAXSIZE];
int curlen;
} SeqString;
定义一个串变量:SeqString s。这种存储方式可以直接得到串的长度:s.curlen+1。如图4.1 所示。
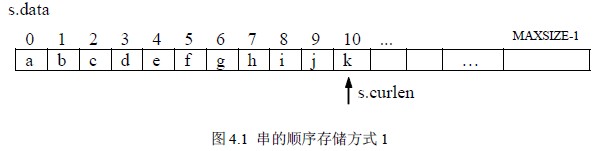 2. 在串尾存储一个不会在串中出现的特殊字符作为串的终结符,以此表示串的结尾。比如C 语言中处理定长串的方法就是这样的,它是用’\0’来表示串的结束。这种存储方法不能直接得到串的长度,是用判断当前字符是否是’\0’来确定串是否结束,从而求得串的长度。
2. 在串尾存储一个不会在串中出现的特殊字符作为串的终结符,以此表示串的结尾。比如C 语言中处理定长串的方法就是这样的,它是用’\0’来表示串的结束。这种存储方法不能直接得到串的长度,是用判断当前字符是否是’\0’来确定串是否结束,从而求得串的长度。
 3. 设定长串存储空间:char s[MAXSIZE+1]; 用s[0]存放串的实际长度,串值存放在s[1]~s[MAXSIZE],字符的序号和存储位置一致,应用更为方便。
3. 设定长串存储空间:char s[MAXSIZE+1]; 用s[0]存放串的实际长度,串值存放在s[1]~s[MAXSIZE],字符的序号和存储位置一致,应用更为方便。
本小节主要讨论定长串联接、求子串、串比较算法,顺序串的插入和删除等运算基本与顺序表相同,在此不在赘述。串定位在下一小节讨论,设串结束用'\0'来标识。
1.串联接:把两个串s1 和s2 首尾连接成一个新串s ,即:s<=s1+s2。
int StrConcat1(s1,s2,s)
char s1[],s2[],s[];
{ int i=0 , j, len1, len2;
len1= StrLength(s1); len2= StrLength(s2)
if (len1+ len2>MAXSIZE-1) return 0 ; /* s 长度不够*/
j=0;
while(s1[j]!=’\0’) { s[i]=s1[j];i++; j++; }
j=0;
while(s2[j]!=’\0’) { s[i]=s2[j];i++; j++; }
s[i]=’\0’; return 1;
}
算法4.1
2.求子串
int StrSub (char *t, char *s, int i, int len)
/* 用t 返回串s 中第个i 字符开始的长度为len 的子串1≤i≤串长*/
{ int slen;
slen=StrLength(s);
if ( i<1 || i>slen || len<0 || len>slen-i+1)
{ printf("参数不对"); return 0; }
for (j=0; j<len; j++)
t[j]=s[i+j-1];
t[j]=’\0’;
return 1;
}
算法4.2
3.串比较
int StrComp(char *s1, char *s2)
{ int i=0;
while (s1[i]==s2[i] && s1[i]!=’\0’) i++;
return (s1[i]-s2[i]);
}
算法4.3
串的模式匹配即子串定位是一种重要的串运算。设s 和t 是给定的两个串,在主串s中找到等于子串t 的过程称为模式匹配,如果在s 中找到等于t 的子串,则称匹配成功,函数返回t 在s 中的首次出现的存储位置(或序号),否则匹配失败,返回-1。t 也称为模式。为了运算方便,设字符串的长度存放在0 号单元,串值从1 号单元存放,这样字符序号与存储位置一致。
1.简单的模式匹配算法
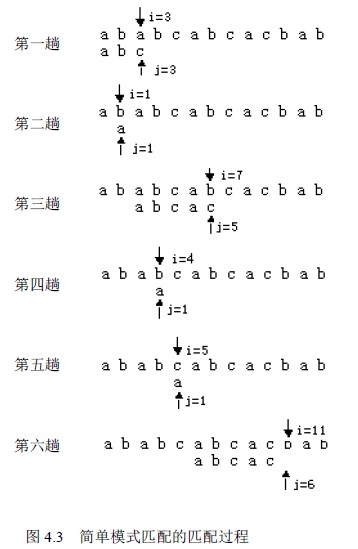
算法思想如下:首先将s1 与t1 进行比较,若不同,就将s2 与t1 进行比较,...,直到s的某一个字符si 和t1 相同,再将它们之后的字符进行比较,若也相同,则如此继续往下比较,当s 的某一个字符si 与t 的字符tj 不同时,则s 返回到本趟开始字符的下一个字符,即si-j+2,t 返回到t1,继续开始下一趟的比较,重复上述过程。若t 中的字符全部比完,则说明本趟匹配成功,本趟的起始位置是i-j+1 或i-t[0],否则,匹配失败。设主串s="ababcabcacbab",模式t="abcac",匹配过程如图4.3 所示。
 依据这个思想,算法描述如下:
依据这个思想,算法描述如下:
int StrIndex_BF (char *s,char *t)
/*从串s 的第一个字符开始找首次与串t 相等的子串*/
{ int i=1,j=1;
while (i<=s[0] && j<=t[0] ) /*都没遇到结束符*/
if (s[i]==t[j])
{ i++;j++; } /*继续*/
else
{i=i-j+2; j=1; } /*回溯*/
if (j>t[0]) return (i-t[0]); /*匹配成功,返回存储位置*/
else return –1;
}
算法4.4
该算法简称为BF 算法。下面分析它的时间复杂度,设串s 长度为n,串t 长度为m。匹配成功的情况下,考虑两种极端情况:在最好情况下,每趟不成功的匹配都发生在第一对字符比较时:
例如:s="aaaaaaaaaabc"
t="bc"
设匹配成功发生在si 处,则字符比较次数在前面i-1 趟匹配中共比较了i-1 次,第i 趟成功的匹配共比较了m 次,所以总共比较了i-1+m 次,所有匹配成功的可能共有n-m+1种,设从si 开始与t 串匹配成功的概率为pi,在等概率情况下pi=1/(n-m+1),因此最好情况下平均比较的次数是:
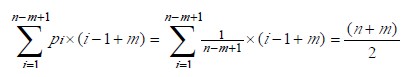 即最好情况下的时间复杂度是O(n+m)。在最坏情况下,每趟不成功的匹配都发生在t 的最后一个字符:
即最好情况下的时间复杂度是O(n+m)。在最坏情况下,每趟不成功的匹配都发生在t 的最后一个字符:
例如:s="aaaaaaaaaaab"
t="aaab"
设匹配成功发生在si 处,则在前面i-1 趟匹配中共比较了(i-1)*m 次,第i 趟成功的匹配共比较了m 次,所以总共比较了i*m 次,因此最坏好情况下平均比较的次数是:
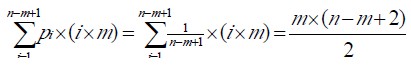 即最坏情况下的时间复杂度是O(n*m)。
即最坏情况下的时间复杂度是O(n*m)。
上述算法中匹配是从s 串的第一个字符开始的,有时算法要求从指定位置开始,这时算法的参数表中要加一个位置参数pos:StrIndex(shar *s,int pos,char *t),比较的初始位置定位在pos 处。算法4.4 是pos=1 的情况。
2.改进后的模式匹配算法
BF 算法简单但效率较低,一种对BF 算法做了很大改进的模式匹配算法是克努特(Knuth),莫里斯(Morris)和普拉特(Pratt)同时设计的,简称KMP 算法。
(1) KMP 算法的思想
分析算法4.4 的执行过程, 造成BF 算法速度慢的原因是回溯,即在某趟的匹配过程失败后,对于s 串要回到本趟开始字符的下一个字符,t 串要回到第一个字符。而这些回溯并不是必要的。如图4.3 所示的匹配过程,在第三趟匹配过程中,s3 ~ s6 和t1~ t4 是匹配成功的,s7≠t5 匹配失败,因此有了第四趟,其实这一趟是不必要的:由图可看出,因为在第三趟中有s4=t2,而t 1≠t2,肯定有t1≠s4 。同理第五趟也是没有必要的,所以从第三趟之后可以直接到第六趟,进一步分析第六趟中的第一对字符s 6 和t1 的比较也是多余的,因为第三趟中已经比过了s6 和t4,并且s6=t4,而t 1=t4,必有s 6=t1,因此第六趟的比较可以从第二对字符s7 和t2 开始进行,这就是说,第三趟匹配失败后,指针i 不动,而是将模式串t向右“滑动”,用t2 “对准” s 7 继续进行,依此类推。这样的处理方法指针i 是无回溯的。
综上所述,希望某趟在si 和tj 匹配失败后,指针i 不回溯,模式t 向右“滑动”至某个位置上,使得tk 对准s i 继续向右进行。显然,现在问题的关键是串t“滑动”到哪个位置上?不妨设位置为k,即si 和tj 匹配失败后,指针i 不动,模式t 向右“滑动”,使tk 和si对准继续向右进行比较,要满足这一假设,就要有如下关系成立:
结论:某趟在si 和tj 匹配失败后,如果模式串中有满足关系(4)的子串存在,即:模式中的前k-1 个字符与模式中tj 字符前面的k-1 个字符相等时,模式t 就可以向右“滑动”至使tk 和si 对准,继续向右进行比较即可。
(2)next 函数
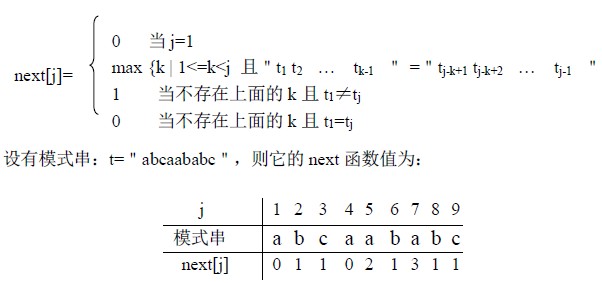
模式中的每一个tj 都对应一个k 值,由(4.4)式可知,这个k 值仅依赖与模式t 本身字符序列的构成,而与主串s 无关。我们用next[j]表示tj 对应的k 值,根据以上分析,next函数有如下性质:
① next[j]是一个整数,且0≤next[j]<j
② 为了使t 的右移不丢失任何匹配成功的可能,当存在多个满足(4.4)式的k 值时,应取最大的,这样向右“滑动”的距离最短,“滑动”的字符为j-next[j]个。
③ 如果在tj 前不存在满足(4.4)式的子串,此时若t1≠tj,则k=1; 若t1=tj,则k=0; 这时“滑动”的最远,为j-1 个字符即用t1 和sj+1 继续比较。
因此,next 函数定义如下:
(3) KMP 算法
在求得模式的next 函数之后,匹配可如下进行:假设以指针i 和j 分别指示主串和模式中的比较字符,令i 的初值为pos,j 的初值为1。若在匹配过程中si≠tj,则i 和j 分别增1,若si≠tj 匹配失败后,则i 不变,j 退到next[j]位置再比较,若相等,则指针各自增1,否则j 再退到下一个next 值的位置,依此类推。直至下列两种情况:一种是j 退到某个next值时字符比较相等,则i 和j 分别增1继续进行匹配; 另一种是j 退到值为零(即模式的第一个字符失配),则此时i 和j 也要分别增1,表明从主串的下一个字符起和模式重新开始匹配。
设主串s="acabaabaabcacaabc",子串t="abaabcac",图4.4 是一个利用next 函数进行匹配的过程示意图。在假设已有next 函数情况下,KMP 算法如下:
int StrIndex_KMP(char *s,char *t,int pos)
/*从串s 的第pos 个字符开始找首次与串t 相等的子串*/
{ int i=pos,j=1,slen,tlen;
while (i<=s[0] && j<=t[0] ) /*都没遇到结束符*/
if (j==0||s[i]==t[j]) { i++; j++; }
else j=next[j]; /*回溯*/
if (j>t[0]) return i-t[0]; /*匹配成功,返回存储位置*/
else return –1;
}
算法4.5

(4)如何求next 函数
由以上讨论知,next 函数值仅取决于模式本身而和主串无关。我们可以从分析next 函数的定义出发用递推的方法求得next 函数值。由定义知:
next[1]=0 (4.5)
设next[j]=k,即有:
第一种情况:若tk =tj 则表明在模式串中
因此: next[j+1]=next[k]+1 (4.11)
同理若t k′ ≠tj,则将模式继续向右滑动至使第next[k′]个字符和tj 对齐,依此类推,直至tj 和模式中的某个字符匹配成功或者不存在任何k′(1< k′<k <…<j)满足(4.10),此时若t1≠tj+1 , 则有:next[j+1]=1 (4.12)
否则若t1=tj+1 ,则有:next[j+1]=0 (4.13)
综上所述,求next 函数值过程的算法如下:
void GetNext(char *t,int next[ ])
/*求模式t 的next 值并寸入next 数组中*/
{ int i=1,j=0;
next[1]=0;
while (i<t[0])
{ while (j>0&&t[i]!=t[j]) j=next[j];
i++; j++;
if (t[i]==t[j]) next[i]=next[j];
else next[i]=j;
}
}
算法4.6
算法4.6 的时间复杂度是O(m);所以算法4.5 的时间复杂度是O(n*m),但在一般情况下,实际的执行时间是O(n+m)。当然KMP 算法和简单的模式匹配算法相比,增加了很大难度,我们主要学习该算法的设计技巧。
4.2.1 串的定长顺序存储
类似于顺序表,用一组地址连续的存储单元存储串值中的字符序列,所谓定长是指按预定义的大小,为每一个串变量分配一个固定长度的存储区,如:
#define MAXSIZE 256
char s[MAXSIZE];
则串的最大长度不能超过256。
如何标识实际长度?
1. 类似顺序表,用一个指针来指向最后一个字符,这样表示的串描述如下:
typedef struct
{ char data[MAXSIZE];
int curlen;
} SeqString;
定义一个串变量:SeqString s。这种存储方式可以直接得到串的长度:s.curlen+1。如图4.1 所示。


4.2.2 定长顺序串的基本运算
本小节主要讨论定长串联接、求子串、串比较算法,顺序串的插入和删除等运算基本与顺序表相同,在此不在赘述。串定位在下一小节讨论,设串结束用'\0'来标识。
1.串联接:把两个串s1 和s2 首尾连接成一个新串s ,即:s<=s1+s2。
int StrConcat1(s1,s2,s)
char s1[],s2[],s[];
{ int i=0 , j, len1, len2;
len1= StrLength(s1); len2= StrLength(s2)
if (len1+ len2>MAXSIZE-1) return 0 ; /* s 长度不够*/
j=0;
while(s1[j]!=’\0’) { s[i]=s1[j];i++; j++; }
j=0;
while(s2[j]!=’\0’) { s[i]=s2[j];i++; j++; }
s[i]=’\0’; return 1;
}
算法4.1
2.求子串
int StrSub (char *t, char *s, int i, int len)
/* 用t 返回串s 中第个i 字符开始的长度为len 的子串1≤i≤串长*/
{ int slen;
slen=StrLength(s);
if ( i<1 || i>slen || len<0 || len>slen-i+1)
{ printf("参数不对"); return 0; }
for (j=0; j<len; j++)
t[j]=s[i+j-1];
t[j]=’\0’;
return 1;
}
算法4.2
3.串比较
int StrComp(char *s1, char *s2)
{ int i=0;
while (s1[i]==s2[i] && s1[i]!=’\0’) i++;
return (s1[i]-s2[i]);
}
算法4.3
4.2.3 模式匹配
串的模式匹配即子串定位是一种重要的串运算。设s 和t 是给定的两个串,在主串s中找到等于子串t 的过程称为模式匹配,如果在s 中找到等于t 的子串,则称匹配成功,函数返回t 在s 中的首次出现的存储位置(或序号),否则匹配失败,返回-1。t 也称为模式。为了运算方便,设字符串的长度存放在0 号单元,串值从1 号单元存放,这样字符序号与存储位置一致。
1.简单的模式匹配算法
算法思想如下:首先将s1 与t1 进行比较,若不同,就将s2 与t1 进行比较,...,直到s的某一个字符si 和t1 相同,再将它们之后的字符进行比较,若也相同,则如此继续往下比较,当s 的某一个字符si 与t 的字符tj 不同时,则s 返回到本趟开始字符的下一个字符,即si-j+2,t 返回到t1,继续开始下一趟的比较,重复上述过程。若t 中的字符全部比完,则说明本趟匹配成功,本趟的起始位置是i-j+1 或i-t[0],否则,匹配失败。设主串s="ababcabcacbab",模式t="abcac",匹配过程如图4.3 所示。

int StrIndex_BF (char *s,char *t)
/*从串s 的第一个字符开始找首次与串t 相等的子串*/
{ int i=1,j=1;
while (i<=s[0] && j<=t[0] ) /*都没遇到结束符*/
if (s[i]==t[j])
{ i++;j++; } /*继续*/
else
{i=i-j+2; j=1; } /*回溯*/
if (j>t[0]) return (i-t[0]); /*匹配成功,返回存储位置*/
else return –1;
}
算法4.4
该算法简称为BF 算法。下面分析它的时间复杂度,设串s 长度为n,串t 长度为m。匹配成功的情况下,考虑两种极端情况:在最好情况下,每趟不成功的匹配都发生在第一对字符比较时:
例如:s="aaaaaaaaaabc"
t="bc"
设匹配成功发生在si 处,则字符比较次数在前面i-1 趟匹配中共比较了i-1 次,第i 趟成功的匹配共比较了m 次,所以总共比较了i-1+m 次,所有匹配成功的可能共有n-m+1种,设从si 开始与t 串匹配成功的概率为pi,在等概率情况下pi=1/(n-m+1),因此最好情况下平均比较的次数是:
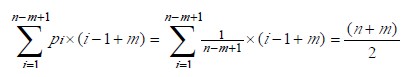
例如:s="aaaaaaaaaaab"
t="aaab"
设匹配成功发生在si 处,则在前面i-1 趟匹配中共比较了(i-1)*m 次,第i 趟成功的匹配共比较了m 次,所以总共比较了i*m 次,因此最坏好情况下平均比较的次数是:
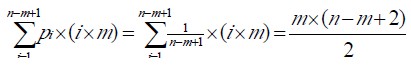
上述算法中匹配是从s 串的第一个字符开始的,有时算法要求从指定位置开始,这时算法的参数表中要加一个位置参数pos:StrIndex(shar *s,int pos,char *t),比较的初始位置定位在pos 处。算法4.4 是pos=1 的情况。
2.改进后的模式匹配算法
BF 算法简单但效率较低,一种对BF 算法做了很大改进的模式匹配算法是克努特(Knuth),莫里斯(Morris)和普拉特(Pratt)同时设计的,简称KMP 算法。
(1) KMP 算法的思想
分析算法4.4 的执行过程, 造成BF 算法速度慢的原因是回溯,即在某趟的匹配过程失败后,对于s 串要回到本趟开始字符的下一个字符,t 串要回到第一个字符。而这些回溯并不是必要的。如图4.3 所示的匹配过程,在第三趟匹配过程中,s3 ~ s6 和t1~ t4 是匹配成功的,s7≠t5 匹配失败,因此有了第四趟,其实这一趟是不必要的:由图可看出,因为在第三趟中有s4=t2,而t 1≠t2,肯定有t1≠s4 。同理第五趟也是没有必要的,所以从第三趟之后可以直接到第六趟,进一步分析第六趟中的第一对字符s 6 和t1 的比较也是多余的,因为第三趟中已经比过了s6 和t4,并且s6=t4,而t 1=t4,必有s 6=t1,因此第六趟的比较可以从第二对字符s7 和t2 开始进行,这就是说,第三趟匹配失败后,指针i 不动,而是将模式串t向右“滑动”,用t2 “对准” s 7 继续进行,依此类推。这样的处理方法指针i 是无回溯的。
综上所述,希望某趟在si 和tj 匹配失败后,指针i 不回溯,模式t 向右“滑动”至某个位置上,使得tk 对准s i 继续向右进行。显然,现在问题的关键是串t“滑动”到哪个位置上?不妨设位置为k,即si 和tj 匹配失败后,指针i 不动,模式t 向右“滑动”,使tk 和si对准继续向右进行比较,要满足这一假设,就要有如下关系成立:
"t1 t2 … tk-1 " ="si-k+1 si-k+2 … si-1 " (4.1)
(4.1)式左边是tk 前面的k-1 个字符,右边是si 前面的k-1 个字符。而本趟匹配失败是在si 和tj 之处,已经得到的部分匹配结果是:
"t1 t2 … tj-1 " ="si-j+1 si-j+2 … si-1 " (4.2)
因为k<j,所以有:
"tj-k+1 tj-k+2 … tj-1 " ="si-k+1 si-k+2 … si-1 " (4.3)
(4.3)式左边是tj 前面的k-1 个字符,右边是si 前面的k-1 个字符,通过(4.1)和(4.3)得到关系:
"t1 t2 … tk-1 " ="tj-k+1 tj-k+2 … tj-1 " (4.4)
结论:某趟在si 和tj 匹配失败后,如果模式串中有满足关系(4)的子串存在,即:模式中的前k-1 个字符与模式中tj 字符前面的k-1 个字符相等时,模式t 就可以向右“滑动”至使tk 和si 对准,继续向右进行比较即可。
(2)next 函数
模式中的每一个tj 都对应一个k 值,由(4.4)式可知,这个k 值仅依赖与模式t 本身字符序列的构成,而与主串s 无关。我们用next[j]表示tj 对应的k 值,根据以上分析,next函数有如下性质:
① next[j]是一个整数,且0≤next[j]<j
② 为了使t 的右移不丢失任何匹配成功的可能,当存在多个满足(4.4)式的k 值时,应取最大的,这样向右“滑动”的距离最短,“滑动”的字符为j-next[j]个。
③ 如果在tj 前不存在满足(4.4)式的子串,此时若t1≠tj,则k=1; 若t1=tj,则k=0; 这时“滑动”的最远,为j-1 个字符即用t1 和sj+1 继续比较。
因此,next 函数定义如下:

(3) KMP 算法
在求得模式的next 函数之后,匹配可如下进行:假设以指针i 和j 分别指示主串和模式中的比较字符,令i 的初值为pos,j 的初值为1。若在匹配过程中si≠tj,则i 和j 分别增1,若si≠tj 匹配失败后,则i 不变,j 退到next[j]位置再比较,若相等,则指针各自增1,否则j 再退到下一个next 值的位置,依此类推。直至下列两种情况:一种是j 退到某个next值时字符比较相等,则i 和j 分别增1继续进行匹配; 另一种是j 退到值为零(即模式的第一个字符失配),则此时i 和j 也要分别增1,表明从主串的下一个字符起和模式重新开始匹配。
设主串s="acabaabaabcacaabc",子串t="abaabcac",图4.4 是一个利用next 函数进行匹配的过程示意图。在假设已有next 函数情况下,KMP 算法如下:
int StrIndex_KMP(char *s,char *t,int pos)
/*从串s 的第pos 个字符开始找首次与串t 相等的子串*/
{ int i=pos,j=1,slen,tlen;
while (i<=s[0] && j<=t[0] ) /*都没遇到结束符*/
if (j==0||s[i]==t[j]) { i++; j++; }
else j=next[j]; /*回溯*/
if (j>t[0]) return i-t[0]; /*匹配成功,返回存储位置*/
else return –1;
}
算法4.5

(4)如何求next 函数
由以上讨论知,next 函数值仅取决于模式本身而和主串无关。我们可以从分析next 函数的定义出发用递推的方法求得next 函数值。由定义知:
next[1]=0 (4.5)
设next[j]=k,即有:
"t1 t2 … tk-1 " ="tj-k+1 tj-k+2 … tj-1 " (4.6)
next[j+1]=? 可能有两种情况:第一种情况:若tk =tj 则表明在模式串中
"t1 t2 … tk " ="tj-k+1 tj-k+2 … tj " (4.7)
这就是说next[j+1]=k+1,即
next[j+1]=next[j]+1 (4.8)
第二种情况:若tk ≠tj 则表明在模式串中
"t1 t2 … tk "≠"tj-k+1 tj-k+2 … tj " (4.9)
此时可把求next 函数值的问题看成是一个模式匹配问题,整个模式串既是主串又是模式,而当前在匹配的过程中,已有(4.6)式成立,则当tk ≠tj 时应将模式向右滑动,使得第next[k]个字符和“主串”中的第j 个字符相比较。若next[k]=k′,且t k′=tj,则说明在主串中第j+1 个字符之前存在一个最大长度为k′的子串,使得
"t1 t2 … t k′ "="tj-k′+1 tj- k′+2 … tj " (4.10)
因此: next[j+1]=next[k]+1 (4.11)
同理若t k′ ≠tj,则将模式继续向右滑动至使第next[k′]个字符和tj 对齐,依此类推,直至tj 和模式中的某个字符匹配成功或者不存在任何k′(1< k′<k <…<j)满足(4.10),此时若t1≠tj+1 , 则有:next[j+1]=1 (4.12)
否则若t1=tj+1 ,则有:next[j+1]=0 (4.13)
综上所述,求next 函数值过程的算法如下:
void GetNext(char *t,int next[ ])
/*求模式t 的next 值并寸入next 数组中*/
{ int i=1,j=0;
next[1]=0;
while (i<t[0])
{ while (j>0&&t[i]!=t[j]) j=next[j];
i++; j++;
if (t[i]==t[j]) next[i]=next[j];
else next[i]=j;
}
}
算法4.6
算法4.6 的时间复杂度是O(m);所以算法4.5 的时间复杂度是O(n*m),但在一般情况下,实际的执行时间是O(n+m)。当然KMP 算法和简单的模式匹配算法相比,增加了很大难度,我们主要学习该算法的设计技巧。

