6.5 二叉树的应用—二叉树遍历的应用
在以上讨论的遍历算法中,访问结点的数据域信息,即操作Visite(bt->data)具有更一般的意义,需根据具体问题,对bt 数据进行不同的操作。下面介绍几个遍历操作的典型应用。
Search(bt,x)在bt 为二叉树的根结点指针的二叉树中查找数据元素x。查找成功时返回该结点的指针;查找失败时返回空指针。
算法实现如下,注意遍历算法中的Visite(bt->data)等同于其中的一组操作步骤。
BiTree Search(BiTree bt,elemtype x)
{/*在bt 为根结点指针的二叉树中查找数据元素x*/
BiTree p;
if (bt->data==x) return bt; /*查找成功返回*/
if (bt->lchild!=NULL) return(Search(bt->lchild,x));
/*在bt->lchild 为根结点指针的二叉树中查找数据元素x*/
if (bt->rchild!=NULL) return(Search(bt->rchild,x));
/*在bt->rchild 为根结点指针的二叉树中查找数据元素x*/
return NULL; /*查找失败返回*/
}
算法6.21
(1)顺序存储结构的实现
int CountLeaf1(SqBiTree bt,int k)
{/*一维数组bt[2k-1]为二叉树存储结构,k 为二叉树深度,函数值为叶子数。*/
total=0;
for(i=1;i<=2k-1;i++)
{ if (bt[i]!=0)
{ if ((bt[2i]==0 && bt[2i+1]==0) || (i>(2k-1)/2))
total++;
}
}
return(total);
}
算法6.22
(2)二叉链表存储结构的实现
int CountLeaf2(BiTree bt)
{/*开始时,bt 为根结点所在链结点的指针,返回值为bt 的叶子数*/
if (bt==NULL) return(0);
if (bt->lchild==NULL && bt->rchild==NULL) return(1);
return(CountLeaf2(bt->lchild)+CountLeaf2(bt->rchild));
}
算法6.23
设创建时,按二叉树带空指针的先序次序输入结点值,结点值类型为字符型。输出按中序输出。
CreateBinTree(BinTree *bt)是以二叉链表为存储结构建立一棵二叉树T 的存储,bt为指向二叉树T 根结点指针的指针。设建立时的输入序列为:AB0D00CE00F00。建立如图6.3 (b)所示的二叉树存储。
InOrderOut(bt)为按中序输出二叉树bt 的结点。算法实现如下,注意在创建算法中,遍历算法中的Visite(bt->data)被读入结点、申请空间存储的操作所代替;在输出算法中,遍历算法中的Visite(bt->data)被c 语言中的格式输出语句所代替。
void CreateBinTree(BinTree *T)
{/*以加入结点的先序序列输入,构造二叉链表*/
char ch;
scanf("\n%c",&ch);
if (ch=='0') *T=NULL; /*读入0 时,将相应结点置空*/
else {*T=(BinTNode*)malloc(sizeof(BinTNode)); /*生成结点空间*/
(*T)->data=ch;
CreateBinTree(&(*T)->lchild); /*构造二叉树的左子树*/
CreateBinTree(&(*T)->rchild); /*构造二叉树的右子树*/
}
}
void InOrderOut(BinTree T)
{/*中序遍历输出二叉树T 的结点值*/
if (T)
{ InOrderOut(T->lchild); /*中序遍历二叉树的左子树*/
printf("%3c",T->data); /*访问结点的数据*/
InOrderOut(T->rchild); /*中序遍历二叉树的右子树*/
}
}
main()
{BiTree bt;
CreateBinTree(&bt);
InOrderOut(bt);
}
算法6.24
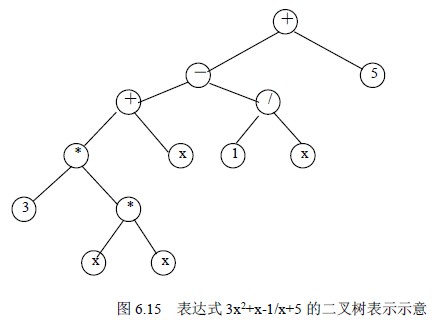
我们可以把任意一个算数表达式用一棵二叉树表示,图6.15 所示为表达式3x2+x-1/x+5的二叉树表示。在表达式二叉树中,每个叶结点都是操作数,每个非叶结点都是运算符。对于一个非叶子结点,它的左、右子树分别是它的两个操作数。
对该二叉树分别进行先序、中序和后序遍历,可以得到表达式的三种不同表示形式。
中缀表达式是经常使用的算术表达式,前缀表达式和后缀表达式分别称为波兰式和逆波兰式,它们在编译程序中有着非常重要的作用。
1.查找数据元素
Search(bt,x)在bt 为二叉树的根结点指针的二叉树中查找数据元素x。查找成功时返回该结点的指针;查找失败时返回空指针。
算法实现如下,注意遍历算法中的Visite(bt->data)等同于其中的一组操作步骤。
BiTree Search(BiTree bt,elemtype x)
{/*在bt 为根结点指针的二叉树中查找数据元素x*/
BiTree p;
if (bt->data==x) return bt; /*查找成功返回*/
if (bt->lchild!=NULL) return(Search(bt->lchild,x));
/*在bt->lchild 为根结点指针的二叉树中查找数据元素x*/
if (bt->rchild!=NULL) return(Search(bt->rchild,x));
/*在bt->rchild 为根结点指针的二叉树中查找数据元素x*/
return NULL; /*查找失败返回*/
}
算法6.21
2.统计出给定二叉树中叶子结点的数目
(1)顺序存储结构的实现
int CountLeaf1(SqBiTree bt,int k)
{/*一维数组bt[2k-1]为二叉树存储结构,k 为二叉树深度,函数值为叶子数。*/
total=0;
for(i=1;i<=2k-1;i++)
{ if (bt[i]!=0)
{ if ((bt[2i]==0 && bt[2i+1]==0) || (i>(2k-1)/2))
total++;
}
}
return(total);
}
算法6.22
(2)二叉链表存储结构的实现
int CountLeaf2(BiTree bt)
{/*开始时,bt 为根结点所在链结点的指针,返回值为bt 的叶子数*/
if (bt==NULL) return(0);
if (bt->lchild==NULL && bt->rchild==NULL) return(1);
return(CountLeaf2(bt->lchild)+CountLeaf2(bt->rchild));
}
算法6.23
3.创建二叉树二叉链表存储,并显示。
设创建时,按二叉树带空指针的先序次序输入结点值,结点值类型为字符型。输出按中序输出。
CreateBinTree(BinTree *bt)是以二叉链表为存储结构建立一棵二叉树T 的存储,bt为指向二叉树T 根结点指针的指针。设建立时的输入序列为:AB0D00CE00F00。建立如图6.3 (b)所示的二叉树存储。
InOrderOut(bt)为按中序输出二叉树bt 的结点。算法实现如下,注意在创建算法中,遍历算法中的Visite(bt->data)被读入结点、申请空间存储的操作所代替;在输出算法中,遍历算法中的Visite(bt->data)被c 语言中的格式输出语句所代替。
void CreateBinTree(BinTree *T)
{/*以加入结点的先序序列输入,构造二叉链表*/
char ch;
scanf("\n%c",&ch);
if (ch=='0') *T=NULL; /*读入0 时,将相应结点置空*/
else {*T=(BinTNode*)malloc(sizeof(BinTNode)); /*生成结点空间*/
(*T)->data=ch;
CreateBinTree(&(*T)->lchild); /*构造二叉树的左子树*/
CreateBinTree(&(*T)->rchild); /*构造二叉树的右子树*/
}
}
void InOrderOut(BinTree T)
{/*中序遍历输出二叉树T 的结点值*/
if (T)
{ InOrderOut(T->lchild); /*中序遍历二叉树的左子树*/
printf("%3c",T->data); /*访问结点的数据*/
InOrderOut(T->rchild); /*中序遍历二叉树的右子树*/
}
}
main()
{BiTree bt;
CreateBinTree(&bt);
InOrderOut(bt);
}
算法6.24
4.表达式运算
我们可以把任意一个算数表达式用一棵二叉树表示,图6.15 所示为表达式3x2+x-1/x+5的二叉树表示。在表达式二叉树中,每个叶结点都是操作数,每个非叶结点都是运算符。对于一个非叶子结点,它的左、右子树分别是它的两个操作数。

对该二叉树分别进行先序、中序和后序遍历,可以得到表达式的三种不同表示形式。
前缀表达式+-+*3*xxx/1x5
中缀表达式3*x*x+x-1/x+5
后缀表达式3xx**x+1x/-5+
中缀表达式3*x*x+x-1/x+5
后缀表达式3xx**x+1x/-5+
中缀表达式是经常使用的算术表达式,前缀表达式和后缀表达式分别称为波兰式和逆波兰式,它们在编译程序中有着非常重要的作用。

