7.1 树的概念与表示
本章是对第六章内容的扩充,即对具有更一般意义的树结构进行讨论。本章所讨论的树结构,其结点可以有任意数目的子结点,这使其在存储以及操作实现上要比二叉树更复杂。
树(Tree)是n(n≥0)个有限数据元素的集合。当n=0 时,称这棵树为空树。在一棵非树T 中:
(1)有一个特殊的数据元素称为树的根结点,根结点没有前驱结点。
(2)若n>1,除根结点之外的其余数据元素被分成m(m>0)个互不相交的集合T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是一棵树。树T1,T2,…,Tm 称为这个根结点的子树。
可以看出,在树的定义中用了递归概念,即用树来定义树。因此,树结构的算法类同于二叉树结构的算法,也可以使用递归方法。
树的定义还可形式化的描述为二元组的形式:
当树为空树时,D=Φ;当树T 不为空树时有:
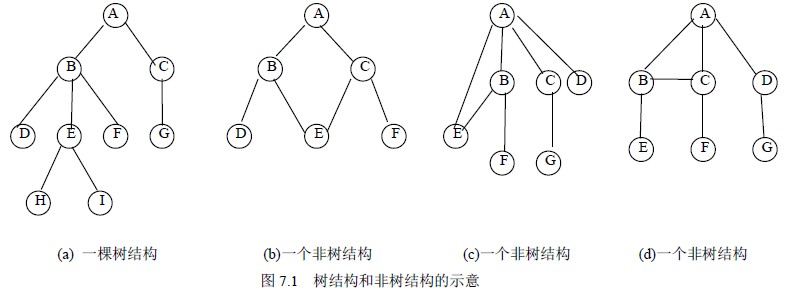
树定义的形式化,主要用于树的理论描述。图7.1(a)是一棵具有9 个结点的树,即T={A,B,C,…,H,I},结点A 为树T 的根结点,除根结点A 之外的其余结点分为两个不相交的集合: T1={B,D,E,F,H,I}和T2={C,G},T1 和T2 构成了结点A 的两棵子树,T1 和T2 本身也分别是一棵树。例如,子树T1 的根结点为B,其余结点又分为两个不相交的集合:T11={D},T12={E,H,I}和T13={F}。
T11、T12 和T13 构成了子树T1 的根结点B 的三棵子树。如此可继续向下分为更小的子树,直到每棵子树只有一个根结点为止。
从树的定义和图7.1(a)的示例可以看出,树具有下面两个特点:
(1)树的根结点没有前驱结点,除根结点之外的所有结点有且只有一个前驱结点。
(2)树中所有结点可以有零个或多个后继结点。
由此特点可知,图7.1(b)、(c)、(d)所示的都不是树结构。
在二叉树中介绍的有关概念在树中仍然适用。除此之外,再介绍两个关于树的术语。
(1)有序树和无序树。如果一棵树中结点的各子树丛左到右是有次序的,即若交换了某结点各子树的相对位置,则构成不同的树,称这棵树为有序树;反之,则称为无序树。
(2)森林。零棵或有限棵不相交的树的集合称为森林。自然界中树和森林是不同的概念,但在数据结构中,树和森林只有很小的差别。任何一棵树,删去根结点就变成了森林。
树的表示方法有以下四种,各用于不同的目的。
1.直观表示法
树的直观表示法就是以倒着的分支树的形式表示,图7.1(a)就是一棵树的直观表示。其特点就是对树的逻辑结构的描述非常直观。是数据结构中最常用的树的描述方法。
2.嵌套集合表示法
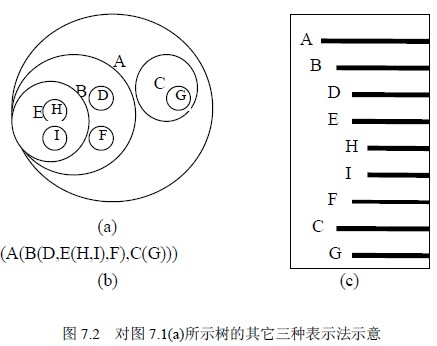
所谓嵌套集合是指一些集合的集体,对于其中任何两个集合,或者不相交,或者一个包含另一个。用嵌套集合的形式表示树,就是将根结点视为一个大的集合,其若干棵子树构成这个大集合中若干个互不相交的子集,如此嵌套下去,即构成一棵树的嵌套集合表示。图7.2 (a)就是一棵树的嵌套集合表示。
3.凹入表示法
树的凹入表示法如图7.2 (c)所示。树的凹入表示法主要用于树的屏幕和打印输出。
4.广义表表示法
树用广义表表示,就是将根作为由子树森林组成的表的名字写在表的左边,这样依次将书表示出来。图7.2 (b)就是一棵树的广义表表示。
7.1.1 树的定义及相关术语
1.树的定义树(Tree)是n(n≥0)个有限数据元素的集合。当n=0 时,称这棵树为空树。在一棵非树T 中:
(1)有一个特殊的数据元素称为树的根结点,根结点没有前驱结点。
(2)若n>1,除根结点之外的其余数据元素被分成m(m>0)个互不相交的集合T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是一棵树。树T1,T2,…,Tm 称为这个根结点的子树。
可以看出,在树的定义中用了递归概念,即用树来定义树。因此,树结构的算法类同于二叉树结构的算法,也可以使用递归方法。
树的定义还可形式化的描述为二元组的形式:
T=(D,R)
其中D 为树T 中结点的集合,R 为树中结点之间关系的集合。当树为空树时,D=Φ;当树T 不为空树时有:
D={Root}∪DF
其中,Root 为树T 的根结点,DF 为树T 的根Root 的子树集合。DF 可由下式表示:
DF=D1∪D2∪…∪Dm 且Di∩Dj=Φ(i≠j,1≤i≤m,1≤j≤m)
当树T 中结点个数n≤1 时,R=Φ;当树T 中结点个数n>1 时有:
R={<Root,ri>,i=1,2,…,m}
其中,Root 为树T 的根结点,ri 是树T 的根结点Root 的子树Ti 的根结点。树定义的形式化,主要用于树的理论描述。图7.1(a)是一棵具有9 个结点的树,即T={A,B,C,…,H,I},结点A 为树T 的根结点,除根结点A 之外的其余结点分为两个不相交的集合: T1={B,D,E,F,H,I}和T2={C,G},T1 和T2 构成了结点A 的两棵子树,T1 和T2 本身也分别是一棵树。例如,子树T1 的根结点为B,其余结点又分为两个不相交的集合:T11={D},T12={E,H,I}和T13={F}。
T11、T12 和T13 构成了子树T1 的根结点B 的三棵子树。如此可继续向下分为更小的子树,直到每棵子树只有一个根结点为止。
从树的定义和图7.1(a)的示例可以看出,树具有下面两个特点:
(1)树的根结点没有前驱结点,除根结点之外的所有结点有且只有一个前驱结点。
(2)树中所有结点可以有零个或多个后继结点。
由此特点可知,图7.1(b)、(c)、(d)所示的都不是树结构。

2.相关术语
在二叉树中介绍的有关概念在树中仍然适用。除此之外,再介绍两个关于树的术语。
(1)有序树和无序树。如果一棵树中结点的各子树丛左到右是有次序的,即若交换了某结点各子树的相对位置,则构成不同的树,称这棵树为有序树;反之,则称为无序树。
(2)森林。零棵或有限棵不相交的树的集合称为森林。自然界中树和森林是不同的概念,但在数据结构中,树和森林只有很小的差别。任何一棵树,删去根结点就变成了森林。
7.1.2 树的表示
树的表示方法有以下四种,各用于不同的目的。
1.直观表示法
树的直观表示法就是以倒着的分支树的形式表示,图7.1(a)就是一棵树的直观表示。其特点就是对树的逻辑结构的描述非常直观。是数据结构中最常用的树的描述方法。
2.嵌套集合表示法
所谓嵌套集合是指一些集合的集体,对于其中任何两个集合,或者不相交,或者一个包含另一个。用嵌套集合的形式表示树,就是将根结点视为一个大的集合,其若干棵子树构成这个大集合中若干个互不相交的子集,如此嵌套下去,即构成一棵树的嵌套集合表示。图7.2 (a)就是一棵树的嵌套集合表示。
3.凹入表示法
树的凹入表示法如图7.2 (c)所示。树的凹入表示法主要用于树的屏幕和打印输出。
4.广义表表示法
树用广义表表示,就是将根作为由子树森林组成的表的名字写在表的左边,这样依次将书表示出来。图7.2 (b)就是一棵树的广义表表示。


