8.2 图的存储表示—邻接矩阵
图是一种结构复杂的数据结构,表现在不仅各个顶点的度可以千差万别,而且顶点之间的逻辑关系也错综复杂。从图的定义可知,一个图的信息包括两部分,即图中顶点的信息以及描述顶点之间的关系――边或者弧的信息。因此无论采用什么方法建立图的存储结构,都要完整、准确地反映这两方面的信息。
下面介绍几种常用的图的存储结构。
所谓邻接矩阵(Adjacency Matrix)的存储结构,就是用一维数组存储图中顶点的信息,用矩阵表示图中各顶点之间的邻接关系。假设图G=(V,E)有n 个确定的顶点,即V={v0,v1,…,vn-1},则表示G 中各顶点相邻关系为一个n×n 的矩阵,矩阵的元素为:

其中,wij 表示边(vi,vj)或<vi,vj>上的权值;∞表示一个计算机允许的、大于所有边上权值的数。
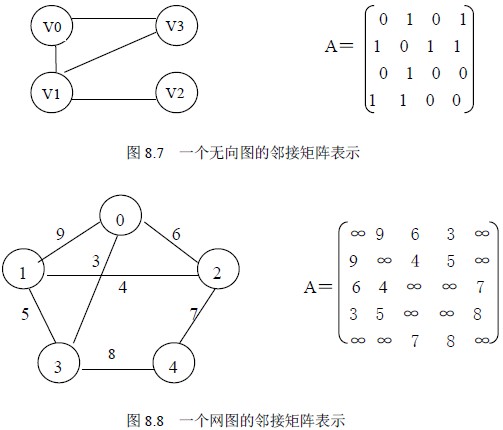
用邻接矩阵表示法表示图如图8.7 所示。
用邻接矩阵表示法表示网图如图8.8 所示。
从图的邻接矩阵存储方法容易看出这种表示具有以下特点:
① 无向图的邻接矩阵一定是一个对称矩阵。因此,在具体存放邻接矩阵时只需存放上(或下)三角矩阵的元素即可。
② 对于无向图,邻接矩阵的第i 行(或第i 列)非零元素(或非∞元素)的个数正好是第i 个顶点的度TD(vi)。
③ 对于有向图,邻接矩阵的第i 行(或第i 列)非零元素(或非∞元素)的个数正好是第i 个顶点的出度OD(vi)(或入度ID(vi))。
④用邻接矩阵方法存储图,很容易确定图中任意两个顶点之间是否有边相连;但是,要确定图中有多少条边,则必须按行、按列对每个元素进行检测,所花费的时间代价很大。
这是用邻接矩阵存储图的局限性。
下面介绍图的邻接矩阵存储表示。
在用邻接矩阵存储图时,除了用一个二维数组存储用于表示顶点间相邻关系的邻接矩阵外,还需用一个一维数组来存储顶点信息,另外还有图的顶点数和边数。故可将其形式描述如下:
#define MaxVertexNum 100 /*最大顶点数设为100*/
typedef char VertexType; /*顶点类型设为字符型*/
typedef int EdgeType; /*边的权值设为整型*/
typedef struct {
VertexType vexs[MaxVertexNum]; /*顶点表*/
EdeType edges[MaxVertexNum][MaxVertexNum]; /*邻接矩阵,即边表*/
int n,e; /*顶点数和边数*/
}Mgragh; /*Maragh 是以邻接矩阵存储的图类型*/
建立一个图的邻接矩阵存储的算法如下:
void CreateMGraph(MGraph *G)
{/*建立有向图G 的邻接矩阵存储*/
int i,j,k,w;
char ch;
printf("请输入顶点数和边数(输入格式为:顶点数,边数):\n");
scanf("%d,%d",&(G->n),&(G->e));/*输入顶点数和边数*/
printf("请输入顶点信息(输入格式为:顶点号<CR>):\n");
for (i=0;i<G->n;i++) scanf("\n%c",&(G->vexs[i])); /*输入顶点信息,建立顶点表*/
for (i=0;i<G->n;i++)
for (j=0;j<G->n;j++) G->edges[i][j]=0; /*初始化邻接矩阵*/
printf("请输入每条边对应的两个顶点的序号(输入格式为:i,j):\n");
for (k=0;k<G->e;k++)
{scanf("\n%d,%d",&i,&j); /*输入e 条边,建立邻接矩阵*/
G->edges[i][j]=1; /*若加入G->edges[j][i]=1;,*/
/*则为无向图的邻接矩阵存储建立*/
}
}/*CreateMGraph*/
算法8.1
下面介绍几种常用的图的存储结构。
所谓邻接矩阵(Adjacency Matrix)的存储结构,就是用一维数组存储图中顶点的信息,用矩阵表示图中各顶点之间的邻接关系。假设图G=(V,E)有n 个确定的顶点,即V={v0,v1,…,vn-1},则表示G 中各顶点相邻关系为一个n×n 的矩阵,矩阵的元素为:

其中,wij 表示边(vi,vj)或<vi,vj>上的权值;∞表示一个计算机允许的、大于所有边上权值的数。
用邻接矩阵表示法表示图如图8.7 所示。
用邻接矩阵表示法表示网图如图8.8 所示。

从图的邻接矩阵存储方法容易看出这种表示具有以下特点:
① 无向图的邻接矩阵一定是一个对称矩阵。因此,在具体存放邻接矩阵时只需存放上(或下)三角矩阵的元素即可。
② 对于无向图,邻接矩阵的第i 行(或第i 列)非零元素(或非∞元素)的个数正好是第i 个顶点的度TD(vi)。
③ 对于有向图,邻接矩阵的第i 行(或第i 列)非零元素(或非∞元素)的个数正好是第i 个顶点的出度OD(vi)(或入度ID(vi))。
④用邻接矩阵方法存储图,很容易确定图中任意两个顶点之间是否有边相连;但是,要确定图中有多少条边,则必须按行、按列对每个元素进行检测,所花费的时间代价很大。
这是用邻接矩阵存储图的局限性。
下面介绍图的邻接矩阵存储表示。
在用邻接矩阵存储图时,除了用一个二维数组存储用于表示顶点间相邻关系的邻接矩阵外,还需用一个一维数组来存储顶点信息,另外还有图的顶点数和边数。故可将其形式描述如下:
#define MaxVertexNum 100 /*最大顶点数设为100*/
typedef char VertexType; /*顶点类型设为字符型*/
typedef int EdgeType; /*边的权值设为整型*/
typedef struct {
VertexType vexs[MaxVertexNum]; /*顶点表*/
EdeType edges[MaxVertexNum][MaxVertexNum]; /*邻接矩阵,即边表*/
int n,e; /*顶点数和边数*/
}Mgragh; /*Maragh 是以邻接矩阵存储的图类型*/
建立一个图的邻接矩阵存储的算法如下:
void CreateMGraph(MGraph *G)
{/*建立有向图G 的邻接矩阵存储*/
int i,j,k,w;
char ch;
printf("请输入顶点数和边数(输入格式为:顶点数,边数):\n");
scanf("%d,%d",&(G->n),&(G->e));/*输入顶点数和边数*/
printf("请输入顶点信息(输入格式为:顶点号<CR>):\n");
for (i=0;i<G->n;i++) scanf("\n%c",&(G->vexs[i])); /*输入顶点信息,建立顶点表*/
for (i=0;i<G->n;i++)
for (j=0;j<G->n;j++) G->edges[i][j]=0; /*初始化邻接矩阵*/
printf("请输入每条边对应的两个顶点的序号(输入格式为:i,j):\n");
for (k=0;k<G->e;k++)
{scanf("\n%d,%d",&i,&j); /*输入e 条边,建立邻接矩阵*/
G->edges[i][j]=1; /*若加入G->edges[j][i]=1;,*/
/*则为无向图的邻接矩阵存储建立*/
}
}/*CreateMGraph*/
算法8.1

