8.3 图的遍历
图的遍历是指从图中的任一顶点出发,对图中的所有顶点访问一次且只访问一次。图的遍历操作和树的遍历操作功能相似。图的遍历是图的一种基本操作,图的许多其它操作都是建立在遍历操作的基础之上。
由于图结构本身的复杂性,所以图的遍历操作也较复杂,主要表现在以下四个方面:
① 在图结构中,没有一个“自然”的首结点,图中任意一个顶点都可作为第一个被访问的结点。
② 在非连通图中,从一个顶点出发,只能够访问它所在的连通分量上的所有顶点,因此,还需考虑如何选取下一个出发点以访问图中其余的连通分量。
③ 在图结构中,如果有回路存在,那么一个顶点被访问之后,有可能沿回路又回到该顶点。
④ 在图结构中,一个顶点可以和其它多个顶点相连,当这样的顶点访问过后,存在如何选取下一个要访问的顶点的问题。
图的遍历通常有深度优先搜索和广度优先搜索两种方式,下面分别介绍。
深度优先搜索(Depth_Fisrst Search)遍历类似于树的先根遍历,是树的先根遍历的推广。
假设初始状态是图中所有顶点未曾被访问,则深度优先搜索可从图中某个顶点发v 出发,访问此顶点,然后依次从v 的未被访问的邻接点出发深度优先遍历图,直至图中所有和v 有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
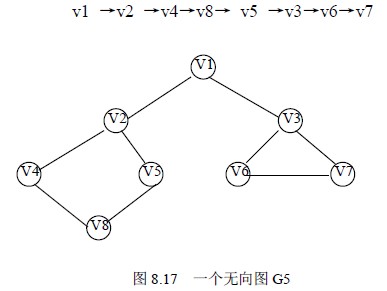
以图8.17 的无向图G5 为例,进行图的深度优先搜索。假设从顶点v1 出发进行搜索,在访问了顶点v1 之后,选择邻接点v2。因为v2 未曾访问,则从v2 出发进行搜索。依次类推,接着从v4 、v8 、v5 出发进行搜索。在访问了v5 之后,由于v5 的邻接点都已被访问,则搜索回到v8。由于同样的理由,搜索继续回到v4,v2 直至v1,此时由于v1 的另一个邻接点未被访问,则搜索又从v1 到v3,再继续进行下去由此,得到的顶点访问序列为:
显然,这是一个递归的过程。为了在遍历过程中便于区分顶点是否已被访问,需附设访问标志数组visited[0:n-1], ,其初值为FALSE ,一旦某个顶点被访问,则其相应的分量置为TRUE。
从图的某一点v 出发,递归地进行深度优先遍历的过程如算法8.4 所示。
void DFS(Graph G,int v )
{ /*从第v 个顶点出发递归地深度优先遍历图G*/
visited[v]=TRUE;VisitFunc(v); /*访问第v 个顶点*/
for(w=FisrAdjVex(G,v);w; w=NextAdjVex(G,v,w))
if (!visited[w]) DFS(G,w); /*对v 的尚未访问的邻接顶点w 递归调用DFS*/
}
算法8.4
算法8.5 和算法8.6 给出了对以邻接表为存储结构的整个图G 进行深度优先遍历实现的C 语言描述。
void DFSTraverseAL(ALGraph *G)
{/*深度优先遍历以邻接表存储的图G*/
int i;
for (i=0;i<G->n;i++)
visited[i]=FALSE; /*标志向量初始化*/
for (i=0;i<G->n;i++)
if (!visited[i]) DFSAL(G,i); /*vi 未访问过,从vi 开始DFS 搜索*/
}/*DFSTraveseAL*/
算法8.5
void DFSAL(ALGraph *G,int i)
{/*以Vi 为出发点对邻接表存储的图G 进行DFS 搜索*/
EdgeNode *p;
printf("visit vertex:V%c\n",G->adjlist[i].vertex);/*访问顶点Vi*/
visited[i]=TRUE; /*标记Vi 已访问*/
p=G->adjlist[i].firstedge; /*取Vi 边表的头指针*/
while(p) /*依次搜索Vi 的邻接点Vj,j=p->adjva*/
{if (!visited[p->adjvex]) /*若Vj 尚未访问,则以Vj 为出发点向纵深搜索*/
DFSAL(G,p->adjvex);
p=p->next; /*找Vi 的下一个邻接点*/
}
}/*DFSAL*/
算法8.6
分析上述算法,在遍历时,对图中每个顶点至多调用一次DFS 函数,因为一旦某个顶点被标志成已被访问,就不再从它出发进行搜索。因此,遍历图的过程实质上是对每个顶点查找其邻接点的过程。其耗费的时间则取决于所采用的存储结构。当用二维数组表示邻接矩阵图的存储结构时,查找每个顶点的邻接点所需时间为O(n2) ,其中n 为图中顶点数。而当以邻接表作图的存储结构时,找邻接点所需时间为O(e),其中e 为无向图中边的数或有向图中弧的数。由此,当以邻接表作存储结构时,深度优先搜索遍历图的时间复杂度为O(n+e) 。
广度优先搜索(Breadth_First Search) 遍历类似于树的按层次遍历的过程。假设从图中某顶点v 出发,在访问了v 之后依次访问v 的各个未曾访问过和邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程中以v 为起始点,由近至远,依次访问和v 有路径相通且路径长度为1,2,…的顶点。
例如,对图8.17 所示无向图G5 进行广度优先搜索遍历,首先访问v1 和v1 的邻接点v2 和v3,然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7,最后访问v4 的邻接点v8。由于这些顶点的邻接点均已被访问,并且图中所有顶点都被访问,由些完成了图的遍历。得到的顶点访问序列为:
和深度优先搜索类似,在遍历的过程中也需要一个访问标志数组。并且,为了顺次访问路径长度为2、3、…的顶点,需附设队列以存储已被访问的路径长度为1、2、… 的顶点。
从图的某一点v 出发,递归地进行广度优先遍历的过程如算法8.7 所示。
void BFSTraverse(Graph G, Status(*Visit)(int v))
{/*按广度优先非递归遍历图G。使用辅助队列Q 和访问标志数组visited*/
for (v=0;v<G,vexnum;++v)
visited[v]=FALSE
InitQueue(Q); /*置空的国债队列Q*/
if (!visited[v]) /*v 尚未访问*/
{EnQucue(Q,v); /*v 入队列*/
while (!QueueEmpty(Q))
{ DeQueue(Q,u); /*队头元素出队并置为u*/
visited[u]=TRUE; visit(u); /*访问u*/
for(w=FistAdjVex(G,u); w; w=NextAdjVex(G,u,w))
if (!visited[w]) EnQueue(Q,w); /*u 的尚未访问的邻接顶点w 入队列Q*/
}
}
}/*BFSTraverse*/
算法8.7
算法8.8 和算法8.9 给出了对以邻接矩阵为存储结构的整个图G 进行深度优先遍历实现的C 语言描述。
void BFSTraverseAL(MGraph *G)
{/*广度优先遍历以邻接矩阵存储的图G*/
int i;
for (i=0;i<G->n;i++)
visited[i]=FALSE; /*标志向量初始化*/
for (i=0;i<G->n;i++)
if (!visited[i]) BFSM(G,i); /* vi 未访问过,从vi 开始BFS 搜索*/
}/*BFSTraverseAL*/
算法8.8
void BFSM(MGraph *G,int k)
{/*以Vi 为出发点,对邻接矩阵存储的图G 进行BFS 搜索*/
int i,j;
CirQueue Q;
InitQueue(&Q);
printf("visit vertex:V%c\n",G->vexs[k]); /*访问原点Vk*/
visited[k]=TRUE;
EnQueue(&Q,k); /*原点Vk 入队列*/
while (!QueueEmpty(&Q))
{i=DeQueue(&Q); /*Vi 出队列*/
for (j=0;j<G->n;j++) /*依次搜索Vi 的邻接点Vj*/
if (G->edges[i][j]==1 && !visited[j]) /*若Vj 未访问*/
{printf("visit vertex:V%c\n",G->vexs[j]); /*访问Vj */
visited[j]=TRUE;
EnQueue(&Q,j); /*访问过的Vj 入队列*/
}
}
}/*BFSM*/
算法8.9
分析上述算法,每个顶点至多进一次队列。遍历图的过程实质是通过边或弧找邻接点的过程,因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同,两者不同之处仅仅在于对顶点访问的顺序不同。
由于图结构本身的复杂性,所以图的遍历操作也较复杂,主要表现在以下四个方面:
① 在图结构中,没有一个“自然”的首结点,图中任意一个顶点都可作为第一个被访问的结点。
② 在非连通图中,从一个顶点出发,只能够访问它所在的连通分量上的所有顶点,因此,还需考虑如何选取下一个出发点以访问图中其余的连通分量。
③ 在图结构中,如果有回路存在,那么一个顶点被访问之后,有可能沿回路又回到该顶点。
④ 在图结构中,一个顶点可以和其它多个顶点相连,当这样的顶点访问过后,存在如何选取下一个要访问的顶点的问题。
图的遍历通常有深度优先搜索和广度优先搜索两种方式,下面分别介绍。
8.3.1 深度优先搜索
深度优先搜索(Depth_Fisrst Search)遍历类似于树的先根遍历,是树的先根遍历的推广。
假设初始状态是图中所有顶点未曾被访问,则深度优先搜索可从图中某个顶点发v 出发,访问此顶点,然后依次从v 的未被访问的邻接点出发深度优先遍历图,直至图中所有和v 有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
以图8.17 的无向图G5 为例,进行图的深度优先搜索。假设从顶点v1 出发进行搜索,在访问了顶点v1 之后,选择邻接点v2。因为v2 未曾访问,则从v2 出发进行搜索。依次类推,接着从v4 、v8 、v5 出发进行搜索。在访问了v5 之后,由于v5 的邻接点都已被访问,则搜索回到v8。由于同样的理由,搜索继续回到v4,v2 直至v1,此时由于v1 的另一个邻接点未被访问,则搜索又从v1 到v3,再继续进行下去由此,得到的顶点访问序列为:

显然,这是一个递归的过程。为了在遍历过程中便于区分顶点是否已被访问,需附设访问标志数组visited[0:n-1], ,其初值为FALSE ,一旦某个顶点被访问,则其相应的分量置为TRUE。
从图的某一点v 出发,递归地进行深度优先遍历的过程如算法8.4 所示。
void DFS(Graph G,int v )
{ /*从第v 个顶点出发递归地深度优先遍历图G*/
visited[v]=TRUE;VisitFunc(v); /*访问第v 个顶点*/
for(w=FisrAdjVex(G,v);w; w=NextAdjVex(G,v,w))
if (!visited[w]) DFS(G,w); /*对v 的尚未访问的邻接顶点w 递归调用DFS*/
}
算法8.4
算法8.5 和算法8.6 给出了对以邻接表为存储结构的整个图G 进行深度优先遍历实现的C 语言描述。
void DFSTraverseAL(ALGraph *G)
{/*深度优先遍历以邻接表存储的图G*/
int i;
for (i=0;i<G->n;i++)
visited[i]=FALSE; /*标志向量初始化*/
for (i=0;i<G->n;i++)
if (!visited[i]) DFSAL(G,i); /*vi 未访问过,从vi 开始DFS 搜索*/
}/*DFSTraveseAL*/
算法8.5
void DFSAL(ALGraph *G,int i)
{/*以Vi 为出发点对邻接表存储的图G 进行DFS 搜索*/
EdgeNode *p;
printf("visit vertex:V%c\n",G->adjlist[i].vertex);/*访问顶点Vi*/
visited[i]=TRUE; /*标记Vi 已访问*/
p=G->adjlist[i].firstedge; /*取Vi 边表的头指针*/
while(p) /*依次搜索Vi 的邻接点Vj,j=p->adjva*/
{if (!visited[p->adjvex]) /*若Vj 尚未访问,则以Vj 为出发点向纵深搜索*/
DFSAL(G,p->adjvex);
p=p->next; /*找Vi 的下一个邻接点*/
}
}/*DFSAL*/
算法8.6
分析上述算法,在遍历时,对图中每个顶点至多调用一次DFS 函数,因为一旦某个顶点被标志成已被访问,就不再从它出发进行搜索。因此,遍历图的过程实质上是对每个顶点查找其邻接点的过程。其耗费的时间则取决于所采用的存储结构。当用二维数组表示邻接矩阵图的存储结构时,查找每个顶点的邻接点所需时间为O(n2) ,其中n 为图中顶点数。而当以邻接表作图的存储结构时,找邻接点所需时间为O(e),其中e 为无向图中边的数或有向图中弧的数。由此,当以邻接表作存储结构时,深度优先搜索遍历图的时间复杂度为O(n+e) 。
8.3.2 广度优先搜索
广度优先搜索(Breadth_First Search) 遍历类似于树的按层次遍历的过程。假设从图中某顶点v 出发,在访问了v 之后依次访问v 的各个未曾访问过和邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程中以v 为起始点,由近至远,依次访问和v 有路径相通且路径长度为1,2,…的顶点。
例如,对图8.17 所示无向图G5 进行广度优先搜索遍历,首先访问v1 和v1 的邻接点v2 和v3,然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7,最后访问v4 的邻接点v8。由于这些顶点的邻接点均已被访问,并且图中所有顶点都被访问,由些完成了图的遍历。得到的顶点访问序列为:
v1→v2 →v3 →v4→ v5→ v6→ v7 →v8
和深度优先搜索类似,在遍历的过程中也需要一个访问标志数组。并且,为了顺次访问路径长度为2、3、…的顶点,需附设队列以存储已被访问的路径长度为1、2、… 的顶点。
从图的某一点v 出发,递归地进行广度优先遍历的过程如算法8.7 所示。
void BFSTraverse(Graph G, Status(*Visit)(int v))
{/*按广度优先非递归遍历图G。使用辅助队列Q 和访问标志数组visited*/
for (v=0;v<G,vexnum;++v)
visited[v]=FALSE
InitQueue(Q); /*置空的国债队列Q*/
if (!visited[v]) /*v 尚未访问*/
{EnQucue(Q,v); /*v 入队列*/
while (!QueueEmpty(Q))
{ DeQueue(Q,u); /*队头元素出队并置为u*/
visited[u]=TRUE; visit(u); /*访问u*/
for(w=FistAdjVex(G,u); w; w=NextAdjVex(G,u,w))
if (!visited[w]) EnQueue(Q,w); /*u 的尚未访问的邻接顶点w 入队列Q*/
}
}
}/*BFSTraverse*/
算法8.7
算法8.8 和算法8.9 给出了对以邻接矩阵为存储结构的整个图G 进行深度优先遍历实现的C 语言描述。
void BFSTraverseAL(MGraph *G)
{/*广度优先遍历以邻接矩阵存储的图G*/
int i;
for (i=0;i<G->n;i++)
visited[i]=FALSE; /*标志向量初始化*/
for (i=0;i<G->n;i++)
if (!visited[i]) BFSM(G,i); /* vi 未访问过,从vi 开始BFS 搜索*/
}/*BFSTraverseAL*/
算法8.8
void BFSM(MGraph *G,int k)
{/*以Vi 为出发点,对邻接矩阵存储的图G 进行BFS 搜索*/
int i,j;
CirQueue Q;
InitQueue(&Q);
printf("visit vertex:V%c\n",G->vexs[k]); /*访问原点Vk*/
visited[k]=TRUE;
EnQueue(&Q,k); /*原点Vk 入队列*/
while (!QueueEmpty(&Q))
{i=DeQueue(&Q); /*Vi 出队列*/
for (j=0;j<G->n;j++) /*依次搜索Vi 的邻接点Vj*/
if (G->edges[i][j]==1 && !visited[j]) /*若Vj 未访问*/
{printf("visit vertex:V%c\n",G->vexs[j]); /*访问Vj */
visited[j]=TRUE;
EnQueue(&Q,j); /*访问过的Vj 入队列*/
}
}
}/*BFSM*/
算法8.9
分析上述算法,每个顶点至多进一次队列。遍历图的过程实质是通过边或弧找邻接点的过程,因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同,两者不同之处仅仅在于对顶点访问的顺序不同。

