8.4 图的连通性—生成树和生成森林
在这一小节里,我们将给出通过对图的遍历,得到图的生成树或生成森林的算法。
设E(G)为连通图G 中所有边的集合,则从图中任一顶点出发遍历图时,必定将E(G)分成两个集合T(G)和B(G),其中T(G)是遍历图过程中历经的边的集合;B(G)是剩余的边的集合。显然,T(G)和图G 中所有顶点一起构成连通图G 的极小连通子图。按照8.1.2 节的定义,它是连通图的一棵生成树,并且由深度优先搜索得到的为深度优先生成树;由广度优先搜索得到的为广度优先生成树。例如,图8.17(a)和(b)所示分别为连通图G5 的深度优先生成树和广度优先生成树。图中虚线为集合B(G) 中的边,实线为集合T(G)中的边。
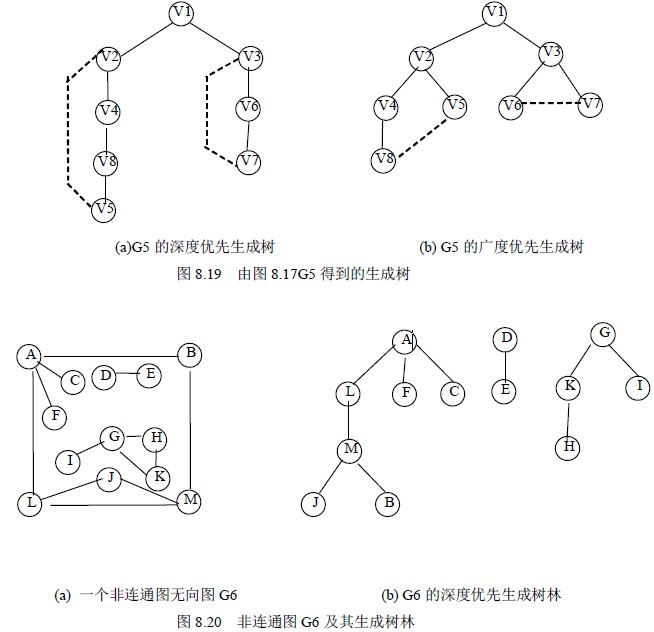
对于非连通图,通过这样的遍历,将得到的是生成森林。例如,图8.20 (b) 所示为图8.20 (a)的深度优先生成森林,它由三棵深度优先生成树组成。
假设以孩子兄弟链表作生成森林的存储结构,则算法8.10 生成非连通图的深度优先生成森林,其中DFSTree 函数如算法8.11 所示。显然,算法8.10 的时间复杂度和遍历相同。
void DESForest(Graph G, CSTree *T)
{ /*建立无向图G 的深度优先生成森林的孩子兄弟链表T*/
T=NULL;
for (v=0;v<G.vexnum;++v)
if (!visited[v]=FALSE;
for(v=0;v<G.vexnum;++v)
if (!visited[v]) /*顶点v 为新的生成树的根结点*/
{ p=(CSTree)malloc(sixeof(CSNode)); /*分配根结点*/
p={GetVex(G,v).NULL,NULL}; /*给根结点赋值*/
if (!T)
(*T)=p; /*T 是第一棵生成树的根*/
else q->nextsibling=p; /*前一棵的根的兄弟是其它生成树的根*/
q=p; /*q 指示当前生成树的根*/
DFSTree(G,v,&p); /*建立以p 为根的生成树*/
}
}
算法8.10
void DFSTree(Graph G,int v ,CSTree *T)
{/*从第v 个顶点出发深度优先遍历图G,建立以*T 为根的生成树*/
visited[v]=TRUE;
first=TRUE;
for(w=FirstAdjVex(G,v); w; w=NextAdjVex(G,v,w))
if(!visited[w])
{ p=(CSTree)malloc(sizeof)CSNode)); /*分配孩子结点*/
*p={GetVex(G,w),NULL,NULL};
if (first) /*w 是v 的第一个未被访问的邻接顶点,作为根的左孩子结点*/
{ T->lchild=p;
first=FALSE;
}
else { /*w 是v 的其它未被访问的邻接顶点,作为上一邻接顶点的右兄弟*/
q->nextsibling=p;
}
q=p;
DFSTree(G,w,&q); /*从第w 个顶点出发深度优先遍历图G,建立生成子树*q*/
}
}
算法8.11
设E(G)为连通图G 中所有边的集合,则从图中任一顶点出发遍历图时,必定将E(G)分成两个集合T(G)和B(G),其中T(G)是遍历图过程中历经的边的集合;B(G)是剩余的边的集合。显然,T(G)和图G 中所有顶点一起构成连通图G 的极小连通子图。按照8.1.2 节的定义,它是连通图的一棵生成树,并且由深度优先搜索得到的为深度优先生成树;由广度优先搜索得到的为广度优先生成树。例如,图8.17(a)和(b)所示分别为连通图G5 的深度优先生成树和广度优先生成树。图中虚线为集合B(G) 中的边,实线为集合T(G)中的边。

对于非连通图,通过这样的遍历,将得到的是生成森林。例如,图8.20 (b) 所示为图8.20 (a)的深度优先生成森林,它由三棵深度优先生成树组成。
假设以孩子兄弟链表作生成森林的存储结构,则算法8.10 生成非连通图的深度优先生成森林,其中DFSTree 函数如算法8.11 所示。显然,算法8.10 的时间复杂度和遍历相同。
void DESForest(Graph G, CSTree *T)
{ /*建立无向图G 的深度优先生成森林的孩子兄弟链表T*/
T=NULL;
for (v=0;v<G.vexnum;++v)
if (!visited[v]=FALSE;
for(v=0;v<G.vexnum;++v)
if (!visited[v]) /*顶点v 为新的生成树的根结点*/
{ p=(CSTree)malloc(sixeof(CSNode)); /*分配根结点*/
p={GetVex(G,v).NULL,NULL}; /*给根结点赋值*/
if (!T)
(*T)=p; /*T 是第一棵生成树的根*/
else q->nextsibling=p; /*前一棵的根的兄弟是其它生成树的根*/
q=p; /*q 指示当前生成树的根*/
DFSTree(G,v,&p); /*建立以p 为根的生成树*/
}
}
算法8.10
void DFSTree(Graph G,int v ,CSTree *T)
{/*从第v 个顶点出发深度优先遍历图G,建立以*T 为根的生成树*/
visited[v]=TRUE;
first=TRUE;
for(w=FirstAdjVex(G,v); w; w=NextAdjVex(G,v,w))
if(!visited[w])
{ p=(CSTree)malloc(sizeof)CSNode)); /*分配孩子结点*/
*p={GetVex(G,w),NULL,NULL};
if (first) /*w 是v 的第一个未被访问的邻接顶点,作为根的左孩子结点*/
{ T->lchild=p;
first=FALSE;
}
else { /*w 是v 的其它未被访问的邻接顶点,作为上一邻接顶点的右兄弟*/
q->nextsibling=p;
}
q=p;
DFSTree(G,w,&q); /*从第w 个顶点出发深度优先遍历图G,建立生成子树*q*/
}
}
算法8.11

