8.4 图的连通性—关节点和重连通分量
假若在删去顶点v 以及和v 相关联的各边之后,将图的一个连通分量分割成两个或两个以上的连通分量,则称顶点v 为该图的一个关节点(articulation point) 。一个没有关节点的连通图称为重连通图(biconnected graph) 。在重连通图上,任意一对顶点之间至少存在两条路径,则在删去某个顶点以及依附于该顶点的各边时也不破坏图的连通性。若在连通图上至少删去k 个顶点才能破坏图的连通性,则称此图的连通度为k。关节点和重连通图在实际中较多应用。显然,一个表示通信网络的图的连通度越高,其系统越可靠,无论是哪一个站点出现故障或遭到外界破坏,都不影响系统的正常工作;又如,一个航空网若是重连通的,则当某条航线因天气等某种原因关闭时,旅客仍可从别的航线绕道而行;再如,若将大规模的集成电路的关键线路设计成重连通的话,则在某些元件失效的情况下,整个片子的功能不受影响,反之,在战争中,若要摧毁敌方的运输线,仅需破坏其运输网中的关节点即可。
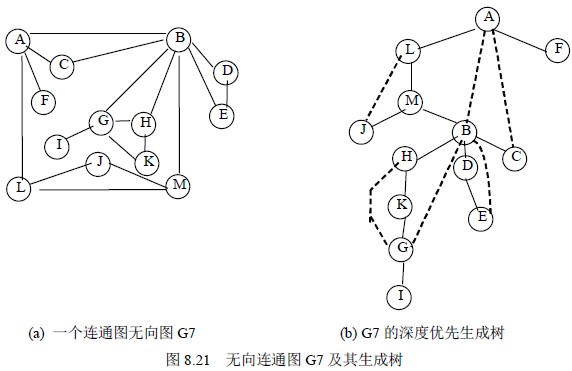
例如,图8.21 (a)中图G7 是连通图,但不是重连通图。图中有四个关节点A、B 和G 。若删去顶点B 以及所有依附顶点B 的边,G7 就被分割成三个连通分量{A、C、F、L、M、J}、{G、H、I、K}和{D、E}。类似地,若删去顶点A 或D 或G 以及所依附于它们的边,则G7 被分割成两个连通分量,由此,关节点亦称为割点。
利用深度优先搜索便可求得图的关节点,并由此可判别图是否是重连通的。
图8.21 (b)所示为从顶点A 出发深优先生成树,图中实线表示树边,虚线表示回边(即不在生成树上的边)。对树中任一顶点v 而言,其孩子结点为在它之后搜索到的邻接点,而其双亲结点和由回边连接的祖先结点是在它之前搜索到的邻接点。由深度优先生成树可得出两类关节点的特性:
(1)若生成树的根有两棵或两棵以上的子树,则此根顶点必为关节点。因为图中不存在联结不同子树中顶点的边,因此,若删去根顶点,生成树便变成生成森林。如图8.21(b)中的顶点A。
(2)若生成树中某个非叶子顶点v,其某棵子树的根和子树中的其它结点均没有指向v 的祖先的回边,则v 为关节点。因为,若删去v,则其子树和图的其它部分被分割开来。如图8.21(b)中的顶点B 和G 。
若对图Graph=(V,{Edge}) 重新定义遍历时的访问函数visited,并引入一个新的函数low,则由一次深度优先遍历便可求得连通图中存在的所有关节点。
定义visited[v]为深度优先搜索遍历连通图时访问顶点v 的次序号;定义:

若对于某个顶点v,存在孩子结点w 且low[w]ㄒvisited[v],则该顶点v 必为关节点。因为当w 是v 的孩子结点时,low[w]ㄒvisited[v],表明w 及其子孙均无指向v 的祖先的回边。由定义可知,visited[v]值即为v 在深度优先生成树的前序序列的序号,只需将DFS 函数中头两个语句改为visited[v0]=++count(在DFSTraverse 中设初值count=1)即可;low[v]可由后序遍历深度优先生成树求得,而v 在后序序列中的次序和遍历时退出DFS 函数的次序相同,由此修改深度优先搜索遍历的算法便可得到求关节点的算法(见算法8.12 和算法8.13)。
void FindArticul(ALGraph G)
{ /*连通图G 以邻接表作存储结构,查找并输出G 上全部关节点*/
count=1; /*全局变量count 用于对访问计数*/
visited[0]=1; /*设定邻接表上0 号顶点为生成树的根*/
for(i=1;i<G.vexnum;++i) /*其余顶点尚未访问*/
visited[i]=0;
p=G.adjlist[0].first;
v=p->adjvex;
DFSArticul(g,v); /*从顶点v 出发深度优先查找关节点*/
if(count<G.vexnum) /*生成树的根至少有两棵子树*/
{printf(0,G.adjlist[0].vertex); /*根是关节点,输出*/
while(p->next)
{ p=p->next;
v=p->adjvex;
if(visited[v]==0) DFSArticul(g,v);
}
}
} /*FindArticul*/
算法8.12
void DFSArticul(ALGraph G,int v0)
/*从顶点v0 出发深度优先遍历图G,查找并输出关节点*/
{ visited[v0]=min=++count; /*v0 是第count 个访问的顶点*/
for(p=G.adjlist[v0].firstedge; p; p=p->next;) /*对v0 的每个邻接点检查*/
{ w=p->adjvex; /*w 为v0 的邻接点*/
if(visited[w]==0) /*若w 未曾访问,则w 为v0 的孩子*/
{ DFSArticul(G,w); /*返回前求得low[w]*/
if(low[w]<min)min=low[w];
if(low[w]>=visited[v0]) printf(v0,G.adjlist[v0].vertex); /*输出关节点*/
}
else if(visited[w]<min) min=visited[w]; /*w 已访问,w 是v0 在生成树上的祖先*/
}
low[v0]=min;
}
算法8.13
例如,图G7 中各顶点计算所得visited 和low 的函数值如下所列:
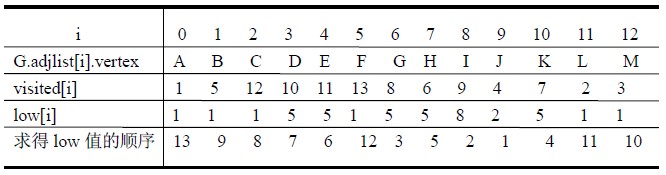
其中J 是第一个求得low 值的顶点,由于存在回边(J,L),则low[J]=Min{visited[J]、visited[L]}=2。顺便提一句,上述算法中将指向双亲的树边也看成是回边,由于不影响关节点的判别,因此,为使算法简明起见,在算法中没有区别之。
由于上述算法的过程就是一个遍历的过程,因此,求关节点的时间复杂度仍为O(n+e)。
例如,图8.21 (a)中图G7 是连通图,但不是重连通图。图中有四个关节点A、B 和G 。若删去顶点B 以及所有依附顶点B 的边,G7 就被分割成三个连通分量{A、C、F、L、M、J}、{G、H、I、K}和{D、E}。类似地,若删去顶点A 或D 或G 以及所依附于它们的边,则G7 被分割成两个连通分量,由此,关节点亦称为割点。

利用深度优先搜索便可求得图的关节点,并由此可判别图是否是重连通的。
图8.21 (b)所示为从顶点A 出发深优先生成树,图中实线表示树边,虚线表示回边(即不在生成树上的边)。对树中任一顶点v 而言,其孩子结点为在它之后搜索到的邻接点,而其双亲结点和由回边连接的祖先结点是在它之前搜索到的邻接点。由深度优先生成树可得出两类关节点的特性:
(1)若生成树的根有两棵或两棵以上的子树,则此根顶点必为关节点。因为图中不存在联结不同子树中顶点的边,因此,若删去根顶点,生成树便变成生成森林。如图8.21(b)中的顶点A。
(2)若生成树中某个非叶子顶点v,其某棵子树的根和子树中的其它结点均没有指向v 的祖先的回边,则v 为关节点。因为,若删去v,则其子树和图的其它部分被分割开来。如图8.21(b)中的顶点B 和G 。
若对图Graph=(V,{Edge}) 重新定义遍历时的访问函数visited,并引入一个新的函数low,则由一次深度优先遍历便可求得连通图中存在的所有关节点。
定义visited[v]为深度优先搜索遍历连通图时访问顶点v 的次序号;定义:

若对于某个顶点v,存在孩子结点w 且low[w]ㄒvisited[v],则该顶点v 必为关节点。因为当w 是v 的孩子结点时,low[w]ㄒvisited[v],表明w 及其子孙均无指向v 的祖先的回边。由定义可知,visited[v]值即为v 在深度优先生成树的前序序列的序号,只需将DFS 函数中头两个语句改为visited[v0]=++count(在DFSTraverse 中设初值count=1)即可;low[v]可由后序遍历深度优先生成树求得,而v 在后序序列中的次序和遍历时退出DFS 函数的次序相同,由此修改深度优先搜索遍历的算法便可得到求关节点的算法(见算法8.12 和算法8.13)。
void FindArticul(ALGraph G)
{ /*连通图G 以邻接表作存储结构,查找并输出G 上全部关节点*/
count=1; /*全局变量count 用于对访问计数*/
visited[0]=1; /*设定邻接表上0 号顶点为生成树的根*/
for(i=1;i<G.vexnum;++i) /*其余顶点尚未访问*/
visited[i]=0;
p=G.adjlist[0].first;
v=p->adjvex;
DFSArticul(g,v); /*从顶点v 出发深度优先查找关节点*/
if(count<G.vexnum) /*生成树的根至少有两棵子树*/
{printf(0,G.adjlist[0].vertex); /*根是关节点,输出*/
while(p->next)
{ p=p->next;
v=p->adjvex;
if(visited[v]==0) DFSArticul(g,v);
}
}
} /*FindArticul*/
算法8.12
void DFSArticul(ALGraph G,int v0)
/*从顶点v0 出发深度优先遍历图G,查找并输出关节点*/
{ visited[v0]=min=++count; /*v0 是第count 个访问的顶点*/
for(p=G.adjlist[v0].firstedge; p; p=p->next;) /*对v0 的每个邻接点检查*/
{ w=p->adjvex; /*w 为v0 的邻接点*/
if(visited[w]==0) /*若w 未曾访问,则w 为v0 的孩子*/
{ DFSArticul(G,w); /*返回前求得low[w]*/
if(low[w]<min)min=low[w];
if(low[w]>=visited[v0]) printf(v0,G.adjlist[v0].vertex); /*输出关节点*/
}
else if(visited[w]<min) min=visited[w]; /*w 已访问,w 是v0 在生成树上的祖先*/
}
low[v0]=min;
}
算法8.13
例如,图G7 中各顶点计算所得visited 和low 的函数值如下所列:

其中J 是第一个求得low 值的顶点,由于存在回边(J,L),则low[J]=Min{visited[J]、visited[L]}=2。顺便提一句,上述算法中将指向双亲的树边也看成是回边,由于不影响关节点的判别,因此,为使算法简明起见,在算法中没有区别之。
由于上述算法的过程就是一个遍历的过程,因此,求关节点的时间复杂度仍为O(n+e)。

