C++堆用法详解
堆(heaps)不是容器,而是一种特别的数据组织方式。堆一般用来保存序列容器。
堆很重要,很多不同的计算机进程中都使用了它们。为了弄明白堆是什么,首先需要明白树是什么,因此首先说明树这种数据结构是什么。
树是分层排列的元素或节点。每个节点有一个键,它是节点中所保存的对象,就如同链表中的节点。父节点是有一个或两个子节点的节点。一般父节点可以有任意个数的子节点,树中的父节点不需要有相同个数的子节点。没有子节点的节点叫作叶节点。一般父节点的键与其子节点有一些关系。树都有一个根节点,它是树的基础,从根节点可以到达所有的子节点。
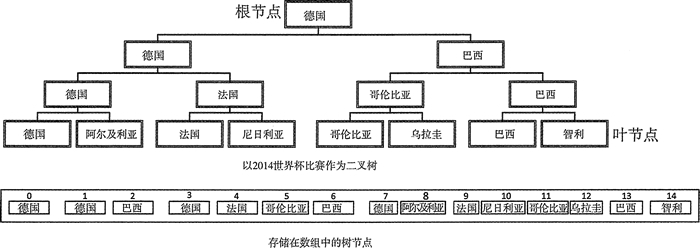
图 1 二叉树示例
图 1 展示了一棵树,它表示 2014 年世界杯最后一组比赛的结果。德国全部赢了,所以它是根节点;它在最后一场比赛中打败了巴西队,所以它和巴西队是它自己的子节点。每个父节点最多有两个子节点的树叫作二叉树。
图 1 中的树是一个完全二叉树,因为每个父节点都有两个子节点。任何树的父节点都有指向子节点的指针。完全二叉树可以用数组的方式保存,也可以用其他顺序表的方式保存,例如 vector,这样就不需要保存子节点的指针,因为知道每一层节点的编号。
如果将每一层树的层数记作 n,从根节点开始作为第 0 层,每一层包含 2n 个节点。图 1 展示了世界杯比赛树的节点如何存储在数组中。每个节点上的整数值是索引值。根节点存放在数组的第一个元素中,后面是它的两个子节点。这对子节点的孩子节点出现在序列的下个位置,以此类推直到叶节点。子节点的索引值为 n,那么它的父节点的索引值就为 (n-1)/2。如果数组元素从 1 开始索引,那么父节点的索引表达式更加简单,它为 n/2。
现在可以定义一个堆:这个堆是一个完全二叉树,每个节点与其子节点位置相对。父节点总是大于或等于子节点,这种情况下被叫作大顶堆,或者父节点总是小于或等于子节点,这种情况下叫作小顶堆。注意,给定父节点的子节点不一定按顺序排列。
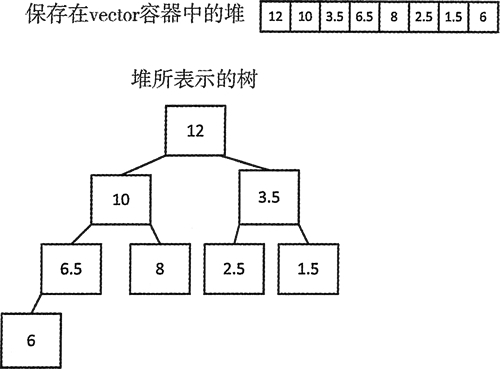
图 2 堆所表示的树
根节点是 12,10 和 3.5 是它的子节点。10 的子节点是 6.5 和 8,3.5 的子节点是 2.5 和 1.5。6.5 只有一个叶节点 6。
priority_queue 是一个堆。在底层,一个 priority_queue 实例创建了一个堆。在堆中,所有成对的连续元素不需要有相同的比较关系。图 2 所示堆中的前 3 个元素是顺序递减的,但第 4 个元素却大于第 3 个元素。既然如此,为什么 STL 有 priority_queue (它是一个堆),却还需要创建堆,特别是还需要将堆作为优先级队列?
这是因为 priority_queue 可以提供堆没有的优势,它可以自动保持元素的顺序;但我们不能打乱 priority_queue 的有序状态,因为除了第一个元素,我们无法直接访问它的其他元素。如果需要的是一个优先级队列,这一点非常有用。
从另一方面来说,使用 make_heap() 创建的堆可以提供一些 priority_queue 没有的优势:
如果使用保持堆顺序的函数,那么可以将堆当作优先级队列使用。
这里有另一个版本的 make_heap(),它有第 3 个参数,可以用来指定一个比较函数用于堆的排序。通过定义一个大于运算符函数,可以生成一个小顶堆。这里可以使用 functional 中的断言。例如:
乍一看,algorithm 中的函数模板 push_heap() 创建堆的方式可能会觉得有些奇怪。为了向堆中添加元素,首先可以用任何方法将元素附加到序列中。然后调用 push_heap() 来插入最后一个元素,为了保持堆的结构,这个元素会被重新排列到一个适当的位置。
push_back() 会在序列末尾添加元素,然后使用 push_heap() 恢复堆的排序。通过调用 push_heap(),释放了一个信号,指出我们向堆中添加了一个元素,这可能会导致堆排序的混乱。push_heap() 会因此认为最后一个元素是新元素,为了保持堆结构,会重新排列序列。
从上面这个示例可以看出,重新排列是有必要的。我们注意到,尽管这个序列是一个堆,但是它的元素并不完全是按降序排列。这清楚地表明,尽管优先级队列是一个堆,但堆元素的顺序并不一定要和优先级队列相同。
当然,也可以用自己的比较函数来创建堆,但是必须和 push_heap() 使用相同的比较函数:
从树来看,显然 6.5 是 6(而不是 10)的子节点,所以这个堆结构是正确的。
删除最大元素和添加元素到堆的过程有些相似,但所做的事是相反的。首先调用 pop_heap(),然后从容器中移除最大的元素,例如:
因为可能会打乱容器中的堆,所以 STL 提供了一个检查序列是否仍然是堆的方法:
甚至可以更深入地检查元素中是否有部分元素为堆。例如:
STL 提供的最后一个操作是 sort_heap(),它会将元素段作为堆来排序。如果元素段不是堆,程序会在运行时崩溃。这个函数有以两个迭代器为参数的版本,迭代器指向一个假定的大顶堆(用 less<> 排列),然后将堆中的元素排成降序。结果当然不再是大顶堆。下面是一个使用它的示例:
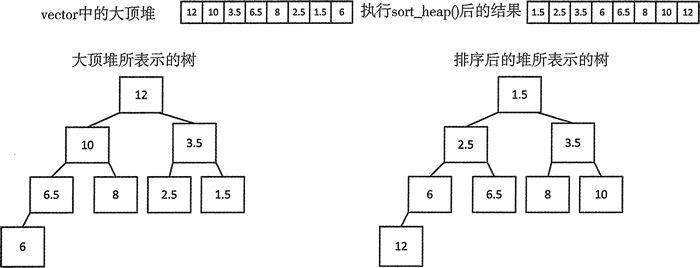
图 4 堆大顶堆排序后生成的小顶堆
第 2 个版本的 sort_heap() 有第 3 个参数,可以指定一个用来创建堆的断言。如果用断言 greater() 来创建堆,会生成一个小顶堆,对它进行排序会生成一个降序序列。排序后的序列不是小顶堆。下面的代码对此做了展示:
我们知道可以用定义在 algorithm 头文件中的函数模板 sort() 来对堆排序,那么为什么还需要 sort_heap() 函数?sort_heap() 函数可以使用特殊的排序算法,巧合的是它被叫作堆排序。这个算法首先会创建一个堆,然后充分利用数据的局部有序性对数据进行排序。sort_heap 认为堆总是存在的,所以它只做上面的第二步操作。充分利用堆的局部有序性可以潜在地使排序变得更快,尽管这可能并不是一直有用。
通过修改上节代码,我们可以用堆作为优先级队列:
通过使用提供的比较函数,max_element() 会返回一个指向最大元素的迭代器。前两个参数是指定序列范围的迭代器。第 3 个参数是一个用于比较运算的 lambda 表达式。
注意,max_dement() 函数需要定义小于而不是大于运算,用来查找最大元素。比较函数的形式如下:
lambda 表达式可以返回字符串的 size() 值的比较结果。max_element() 返回的迭代器指向最长的字符串,因此可以调用它的成员函数 size() 来将它的长度记录到 max_len 中。
用我们之前见过的方式从 cin 中读取单词。这里调用 cin 的成员函数 clear() 来清除 EOF 状态,这个状态是在输入 Ctrl+Z 时设置的。如果不调用 clear(),EOF 状态会继续保留,这样后面就无法再从标准输入流获取输入了。
读入一些单词序列后,通过调用 make_heap() 函数将 deque 容器中的内容排成堆。然后读取一些单词,在将每个单词添加到容器时,需要调用 push_heap() 来保持堆序。push_heap() 希望新元素被添加在容器的尾部;如果使用 push_front(),程序会因此崩溃,因为这时候堆是无效的。输出表明所有代码按预期工作。
当然,如果每次输入单词后,都使用 push_heap(),就不需要调用 make_heap()。该例展示了如何使用我们控制的底层容器来访问全部元素,并且保留它们,而不需要像使用优先级队列那样在使用前不得不先备份它。
堆很重要,很多不同的计算机进程中都使用了它们。为了弄明白堆是什么,首先需要明白树是什么,因此首先说明树这种数据结构是什么。
树是分层排列的元素或节点。每个节点有一个键,它是节点中所保存的对象,就如同链表中的节点。父节点是有一个或两个子节点的节点。一般父节点可以有任意个数的子节点,树中的父节点不需要有相同个数的子节点。没有子节点的节点叫作叶节点。一般父节点的键与其子节点有一些关系。树都有一个根节点,它是树的基础,从根节点可以到达所有的子节点。

图 1 二叉树示例
图 1 展示了一棵树,它表示 2014 年世界杯最后一组比赛的结果。德国全部赢了,所以它是根节点;它在最后一场比赛中打败了巴西队,所以它和巴西队是它自己的子节点。每个父节点最多有两个子节点的树叫作二叉树。
图 1 中的树是一个完全二叉树,因为每个父节点都有两个子节点。任何树的父节点都有指向子节点的指针。完全二叉树可以用数组的方式保存,也可以用其他顺序表的方式保存,例如 vector,这样就不需要保存子节点的指针,因为知道每一层节点的编号。
如果将每一层树的层数记作 n,从根节点开始作为第 0 层,每一层包含 2n 个节点。图 1 展示了世界杯比赛树的节点如何存储在数组中。每个节点上的整数值是索引值。根节点存放在数组的第一个元素中,后面是它的两个子节点。这对子节点的孩子节点出现在序列的下个位置,以此类推直到叶节点。子节点的索引值为 n,那么它的父节点的索引值就为 (n-1)/2。如果数组元素从 1 开始索引,那么父节点的索引表达式更加简单,它为 n/2。
现在可以定义一个堆:这个堆是一个完全二叉树,每个节点与其子节点位置相对。父节点总是大于或等于子节点,这种情况下被叫作大顶堆,或者父节点总是小于或等于子节点,这种情况下叫作小顶堆。注意,给定父节点的子节点不一定按顺序排列。
创建堆
用来创建堆的函数定义在头文件 algorithm 中。max_heap() 对随机访问迭代器指定的一段元素重新排列,生成一个堆。默认使用的是 < 运算符,可以生成一个大顶堆。例如:
std::vector<double>numbers{2.5,10.0,3.5,6.5,8.0,12.0,1.5,6.0};
std::make_heap(std::begin(numbers), std:rend(numbers));
// Result: 12 10 3.5 6.5 8 2.5 1.5 6
调用 make_heap() 后,vector 中的元素如注释所示,这也说明了图 2 所展示的结构。
图 2 堆所表示的树
根节点是 12,10 和 3.5 是它的子节点。10 的子节点是 6.5 和 8,3.5 的子节点是 2.5 和 1.5。6.5 只有一个叶节点 6。
priority_queue 是一个堆。在底层,一个 priority_queue 实例创建了一个堆。在堆中,所有成对的连续元素不需要有相同的比较关系。图 2 所示堆中的前 3 个元素是顺序递减的,但第 4 个元素却大于第 3 个元素。既然如此,为什么 STL 有 priority_queue (它是一个堆),却还需要创建堆,特别是还需要将堆作为优先级队列?
这是因为 priority_queue 可以提供堆没有的优势,它可以自动保持元素的顺序;但我们不能打乱 priority_queue 的有序状态,因为除了第一个元素,我们无法直接访问它的其他元素。如果需要的是一个优先级队列,这一点非常有用。
从另一方面来说,使用 make_heap() 创建的堆可以提供一些 priority_queue 没有的优势:
- 可以访问堆中的任意元素,而不限于最大的元素,因为元素被存储在一个容器中,就像是我们自己的 vector。这也提供了偶然破坏元素顺序的可能,但是总可以调用 make_heap() 来还原堆。
- 可以在任何提供随机访问迭代器的序列容器中创建堆。这些序列容器包括普通数组、string 对象、自定义容器。这意味着无论什么时候需要,都可以用这些序列容器的元素创建堆,必要时,可以反复创建。甚至还可以为元素的子集创建堆。
如果使用保持堆顺序的函数,那么可以将堆当作优先级队列使用。
这里有另一个版本的 make_heap(),它有第 3 个参数,可以用来指定一个比较函数用于堆的排序。通过定义一个大于运算符函数,可以生成一个小顶堆。这里可以使用 functional 中的断言。例如:
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers),
std::greater<>()); // Result: 1.5 6 2.5 6.5 8 12 3.5 10
可以将模板类型参数指定为 greater。这里的这个尖括号为空的版本推断并返回了类型参数。已经有一个用 make_heap() 函数在容器中生成的堆。可以在它上面进行很多操作,下面我们来深入了解这些操作。堆操作
堆不是容器,而是组织容器元素的一种特别方式。只能确定堆的范围,即开始和结束迭代器指定的范围。这意味着可以用容器中的元素子序列创建堆。可以在已生成的堆中添加元素。乍一看,algorithm 中的函数模板 push_heap() 创建堆的方式可能会觉得有些奇怪。为了向堆中添加元素,首先可以用任何方法将元素附加到序列中。然后调用 push_heap() 来插入最后一个元素,为了保持堆的结构,这个元素会被重新排列到一个适当的位置。
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers),std::end(numbers));
// Result: 12 10 3.5 6.5 8 2.5 1.5 6
numbers.push_back(11); // Result: 12 10 3.5 6.5 8 2.5 1.5 6 11
std::push_heap(std::begin(numbers), std::end(numbers));
// Result: 12 11 3. 5 10 8 2. 5 1. 5 6 6. 5
注释显示了每个操作执行后的效果。必须以这种方式向堆中添加元素。只能通过调用成员函数向 queue 中添加新元素,而且这个成员函数只接受迭代器作为参数,不能直接以元素作为参数。push_back() 会在序列末尾添加元素,然后使用 push_heap() 恢复堆的排序。通过调用 push_heap(),释放了一个信号,指出我们向堆中添加了一个元素,这可能会导致堆排序的混乱。push_heap() 会因此认为最后一个元素是新元素,为了保持堆结构,会重新排列序列。
从上面这个示例可以看出,重新排列是有必要的。我们注意到,尽管这个序列是一个堆,但是它的元素并不完全是按降序排列。这清楚地表明,尽管优先级队列是一个堆,但堆元素的顺序并不一定要和优先级队列相同。
当然,也可以用自己的比较函数来创建堆,但是必须和 push_heap() 使用相同的比较函数:
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers),
std::greater<>());//Result: 1.5 6 2.5 6.5 8 12 3.5 10 numbers. push—back(1. 2);
//Result: 1.5 6 2.5 6.5 8 12 3.5 10 1.2
std::push_heap(std::begin(numbers), std::end(numbers),std::greater<>());
//Result: 1.2 1.5 2.5 6 8 12 3.5 10 6.5
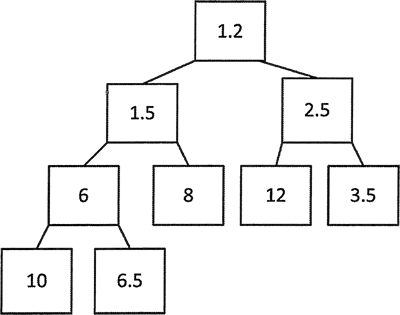
如果 push_heap() 和 make_heap() 的第 3 个参数不同,代码就无法正常执行。注释显示的结果中,最后的 6.5 似乎有些奇怪,图 3 展示的堆树能说明这个问题。
图3 浮点值数堆
从树来看,显然 6.5 是 6(而不是 10)的子节点,所以这个堆结构是正确的。
删除最大元素和添加元素到堆的过程有些相似,但所做的事是相反的。首先调用 pop_heap(),然后从容器中移除最大的元素,例如:
std::vector<double> numbers{2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers),std::end(numbers));
//Result:12 10 3.5 6.5 8 2.5 1.5 6
std::pop_heap(std::begin(numbers),std::end(numbers));
// Result:10 8 3.5 6.5 6 2.5 1.5 12
numbers.pop_back();// Result:10 8 3.5 6.5 6 2.5 1.5
pop_heap() 函数将第一个元素移到最后,并保证剩下的元素仍然是一个堆。然后就可以使用 vector 的成员函数 pop_back() 移除最后一个元素。如果 make_heap() 中用的是自己的比较函数,那么 pop_heap() 的第 3 个参数也需要是这个函数:
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers),std::end(numbers),std::greater<>());
// Result: 1.5 6 2.5 6.5 8 12 3.5 10
std::pop_heap(std::begin(numbers), std::end(numbers),std:: greater<>());
// Result: 2.5 6 3.5 6.5 8 12 10 1.5
numbers.pop_back();//Result: 2.5 6 3.5 6.5 8 12 10
从注释显示的操作结果来看,显然需要为 pop_heap() 提供一个比较运算符函数。pop_heap() 函数不会交换第一个元素和最后一个元素,它会对从 begin(numbers) 到 end(numbers)-1 这个范围内的元素重新排序,从而保持堆的顺序。为了能够正确执行这个操作,pop_heap() 必须和 make_heap() 使用相同的比较函数。因为可能会打乱容器中的堆,所以 STL 提供了一个检查序列是否仍然是堆的方法:
if(std::is_heap(std::begin(numbers),std::end(numbers)))
std::cout << "Great! We still have a heap.\n";
else
std::cout << "oh bother! We messed up the heap.\n";
如果元素段是堆,那么 is_heap() 会返回 true。这里是用默认的比较断言 less<> 来检查元素顺序。如果这里使用的是用 greater<> 创建的堆,就会产生错误的结果。为了得到正确的结果,表达式需要写为:
std::is_heap(std::begin(numbers),std::end(numbers),std::greater<>())。
甚至可以更深入地检查元素中是否有部分元素为堆。例如:
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), ::end(numbers),std:: greater<>());
// Result: 1.5 6 2.5 6.5 8 12 3.5 10
std::pop_heap (std::begin (numbers) , std::end(numbers),std::greater<>());
// Result: 2.5 6 3.5 6.5 8 12 10 1.5
auto iter = std::is_heap_until(std::begin(numbers),std::end(numbers),std::greater<>());
if(iter != std::end(numbers))
std::cout << "numbers is a heap up to "<<*iter<<std::endl;
is_heap_until() 函数返回一个迭代器,指向第一个不在堆内的元素。这个代码段会输出最后一个元素的值 1.5,因为在调用 pop_heap() 后,这个元素就不在堆内了。如果整段元素都是堆,函数会返回一个结束迭代器,因此if语句可以确保我们不会解引用一个结束迭代器。如果这段元素少于两个,也会返回一个结束迭代器。这里还有另一个版本的 is_heap_until(),它有两个参数,以 less<> 作为默认断言。STL 提供的最后一个操作是 sort_heap(),它会将元素段作为堆来排序。如果元素段不是堆,程序会在运行时崩溃。这个函数有以两个迭代器为参数的版本,迭代器指向一个假定的大顶堆(用 less<> 排列),然后将堆中的元素排成降序。结果当然不再是大顶堆。下面是一个使用它的示例:
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers));
//Result: 12 10 3.5 6.5 8 2.5 1.5 6
std::sort_heap(std::begin(numbers), std::end(numbers));
// Result: 1.5 2.5 3.5 6 6.5 8 10 12
排序操作的结果不是一个大顶堆,而是一个小顶堆。如图 4 所示,尽管堆并不是全部有序的,但任何全部有序的序列都是堆。

图 4 堆大顶堆排序后生成的小顶堆
第 2 个版本的 sort_heap() 有第 3 个参数,可以指定一个用来创建堆的断言。如果用断言 greater() 来创建堆,会生成一个小顶堆,对它进行排序会生成一个降序序列。排序后的序列不是小顶堆。下面的代码对此做了展示:
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers),std::greater<>());
// Result: 1.5 6 2.5 6.5 8 12 3.5 10
std::sort_heap(std::begin(numbers), std::end(numbers),std::greater<>());
// Result: 12 10 8 6.5 6 3.5 2.5 1.5
如最后一行注释中显示的那样,对小顶堆执行 sort_heap() 后,会变成一个大顶堆。我们知道可以用定义在 algorithm 头文件中的函数模板 sort() 来对堆排序,那么为什么还需要 sort_heap() 函数?sort_heap() 函数可以使用特殊的排序算法,巧合的是它被叫作堆排序。这个算法首先会创建一个堆,然后充分利用数据的局部有序性对数据进行排序。sort_heap 认为堆总是存在的,所以它只做上面的第二步操作。充分利用堆的局部有序性可以潜在地使排序变得更快,尽管这可能并不是一直有用。
通过修改上节代码,我们可以用堆作为优先级队列:
// Using a heap as a priority queue #include <iostream> // For standard streams #include <iomanip> // For stream manipulators #include <algorithm> // For heap support functions #include <string> // For string class #include <deque> // For deque container using std::string; // List a deque of words void show(const std::deque<string>& words, size_t count = 5) { if(words.empty()) return; // Ensure deque has elements // Find length of longest string auto max_len = std::max_element(std::begin(words), std::end(words), [](const string& s1, const string& s2) {return s1.size() < s2.size(); })->size(); size_t n {count}; for(const auto& word : words) { std::cout << std::setw(max_len + 1) << word << " "; if(--n) continue; std::cout << std::endl; n = count; } std::cout << std::endl; } int main() { std::deque<string> words; std::string word; std::cout << "Enter words separated by spaces, enter Ctrl+Z on a separate line to end:\n"; while (true) { if ((std::cin >> word).eof()) { std::cin.clear(); break; } words.push_back(word); } std::cout << "The words in the list are:" << std::endl; show(words); std::make_heap(std::begin(words), std::end(words)); std::cout << "\nAfter making a heap, the words in the list are:" << std::endl; show(words); std::cout << "\nYou entered " << words.size() << " words. Enter some more:" << std::endl; while (true) { if ((std::cin >> word).eof()) { std::cin.clear(); break; } words.push_back(word); std::push_heap(std::begin(words), std::end(words)); } std::cout << "\nThe words in the list are now:" << std::endl; show(words); }运行结果为:
Enter words separated by spaces, enter Ctrl+Z on a separate line to end:
one two three four five six seven
^Z
The words in the list are:
one two three four five
six seven
After making a heap, the words in the list are:
two one three four five
six seven
You entered 7 words. Enter some more:
eight nine ten twelve fifteen ninety forty fifty-three
^Z
The words in the list are now:
two twelve three nine ten
six seven eight four five
one fifteen ninety forty fifty-three
通过使用提供的比较函数,max_element() 会返回一个指向最大元素的迭代器。前两个参数是指定序列范围的迭代器。第 3 个参数是一个用于比较运算的 lambda 表达式。
注意,max_dement() 函数需要定义小于而不是大于运算,用来查找最大元素。比较函数的形式如下:
bool comp(const T1& a,const T2& b);大多数情况下,第一个参数和第二个参数的类型相同,但有时类型也可以不同。唯一的要求是,这个范围内的元素需要可以隐式转换为 T1、T2 类型。参数不需要指定为 const,但最好这样做。在任何情况下,比较函数都不能改变传给它的参数值。
lambda 表达式可以返回字符串的 size() 值的比较结果。max_element() 返回的迭代器指向最长的字符串,因此可以调用它的成员函数 size() 来将它的长度记录到 max_len 中。
用我们之前见过的方式从 cin 中读取单词。这里调用 cin 的成员函数 clear() 来清除 EOF 状态,这个状态是在输入 Ctrl+Z 时设置的。如果不调用 clear(),EOF 状态会继续保留,这样后面就无法再从标准输入流获取输入了。
读入一些单词序列后,通过调用 make_heap() 函数将 deque 容器中的内容排成堆。然后读取一些单词,在将每个单词添加到容器时,需要调用 push_heap() 来保持堆序。push_heap() 希望新元素被添加在容器的尾部;如果使用 push_front(),程序会因此崩溃,因为这时候堆是无效的。输出表明所有代码按预期工作。
当然,如果每次输入单词后,都使用 push_heap(),就不需要调用 make_heap()。该例展示了如何使用我们控制的底层容器来访问全部元素,并且保留它们,而不需要像使用优先级队列那样在使用前不得不先备份它。
所有教程
- socket
- Python基础教程
- C#教程
- MySQL函数
- MySQL
- C语言入门
- C语言专题
- C语言编译器
- C语言编程实例
- GCC编译器
- 数据结构
- C语言项目案例
- C++教程
- OpenCV
- Qt教程
- Unity 3D教程
- UE4
- STL
- Redis
- Android教程
- JavaScript
- PHP
- Mybatis
- Spring Cloud
- Maven
- vi命令
- Spring Boot
- Spring MVC
- Hibernate
- Linux
- Linux命令
- Shell脚本
- Java教程
- 设计模式
- Spring
- Servlet
- Struts2
- Java Swing
- JSP教程
- CSS教程
- TensorFlow
- 区块链
- Go语言教程
- Docker
- 编程笔记
- 资源下载
- 关于我们
- 汇编语言
- 大数据
- 云计算
- VIP视频
