首页 > Python基础教程 > Python常见模块
阅读:4,616
Python heapq(堆操作)用法详解
Python 提供了关于堆的操作,下面先简单介绍有关堆的概念。
假设有 n 个数据元素的序列 k0,k1,...,kn-1,当且仅当满足
对于满足小顶堆的数据序列 k0,k1,...,kn-1,如果将它们顺序排成一棵完全二叉树,则此树的特点是:树中所有节点的值都小于其左、右子节点的值,此树的根节点的值必然最小。反之,对于满足大顶堆的数据序列 k0,k1,...,kn-1,如果将它们顺序排成一棵完全二叉树,则此树的特点是:树中所有节点的值都大于其左、右子节点的值,此树的根节点的值必然最大。
通过上面介绍不难发现,小顶堆的任意子树也是小顶堆,大顶堆的任意子树还是大顶堆。
Python 提供的是基于小顶堆的操作,因此 Python 可以对 list 中的元素进行小顶堆排列,这样程序每次获取堆中元素时,总会取得堆中最小的元素。
例如,判断数据序列
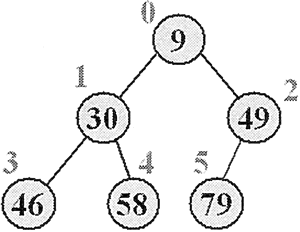
图 1 完全二叉树
在图 1 中,每个节点上的灰色数字代表该节点数据在底层数组中的索引。图 1 所示的完全二叉树完全满足小顶堆的特征,每个父节点的值总小于或等于它的左、右子节点的值。
Python 并没有提供“堆”这种数据类型,它是直接把列表当成堆处理的。Python 提供的 heapq 包中有一些函数,当程序用这些函数来操作列表时,该列表就会表现出“堆”的行为。
在交互式解释器中先导入 heapq 包,然后输入
下面程序示范了这些函数的用法:
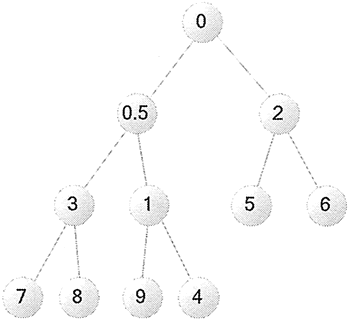
图 2 小顶堆对应的完全二叉树
当程序再次调用 heappush(my_data, 7.2) 向堆中加入一个元素之后,输出该堆中元素,可以看到如下输出结果:
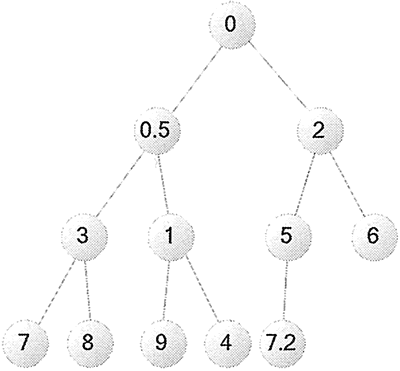
图 3 添加 7.2 之后的小顶堆对应的完全二叉树
接下来程序尝试从堆中弹出两个元素:
下面代码示范了 replace() 函数的用法:
假设有 n 个数据元素的序列 k0,k1,...,kn-1,当且仅当满足
ki≤k2i+1 且 ki≤k2i+2(其中 i=0,2,...,(n-1)/2)时,可以将这组数据称为小顶堆(小根堆);或者满足 ki≥k2i+1 且 ki≥k2i+2(其中 i=0,2,...,(n-1)/2)时,可以将这组数据称为大顶堆(大根堆)。对于满足小顶堆的数据序列 k0,k1,...,kn-1,如果将它们顺序排成一棵完全二叉树,则此树的特点是:树中所有节点的值都小于其左、右子节点的值,此树的根节点的值必然最小。反之,对于满足大顶堆的数据序列 k0,k1,...,kn-1,如果将它们顺序排成一棵完全二叉树,则此树的特点是:树中所有节点的值都大于其左、右子节点的值,此树的根节点的值必然最大。
通过上面介绍不难发现,小顶堆的任意子树也是小顶堆,大顶堆的任意子树还是大顶堆。
Python 提供的是基于小顶堆的操作,因此 Python 可以对 list 中的元素进行小顶堆排列,这样程序每次获取堆中元素时,总会取得堆中最小的元素。
例如,判断数据序列
9, 30, 49, 46, 58, 79 是否为堆,可以将其转换为一棵完全二叉树,如图 1 所示。

图 1 完全二叉树
在图 1 中,每个节点上的灰色数字代表该节点数据在底层数组中的索引。图 1 所示的完全二叉树完全满足小顶堆的特征,每个父节点的值总小于或等于它的左、右子节点的值。
Python 并没有提供“堆”这种数据类型,它是直接把列表当成堆处理的。Python 提供的 heapq 包中有一些函数,当程序用这些函数来操作列表时,该列表就会表现出“堆”的行为。
在交互式解释器中先导入 heapq 包,然后输入
heapq.__all__ 命令来查看 heapq 包下的全部函数,可以看到如下输出结果:
>>> heapq.__all__
['heappush', 'heappop', 'heapify', 'heapreplace', 'merge', 'nlargest', 'nsmallest', 'heappushpop']
- heappush(heap, item):将 item 元素加入堆。
- heappop(heap):将堆中最小元素弹出。
- heapify(heap):将堆属性应用到列表上。
- heapreplace(heap, x):将堆中最小元素弹出,并将元素x 入堆。
- merge(*iterables, key=None, reverse=False):将多个有序的堆合并成一个大的有序堆,然后再输出。
- heappushpop(heap, item):将item 入堆,然后弹出并返回堆中最小的元素。
- nlargest(n, iterable, key=None):返回堆中最大的 n 个元素。
- nsmallest(n, iterable, key=None):返回堆中最小的 n 个元素。
下面程序示范了这些函数的用法:
from heapq import *
my_data = list(range(10))
my_data.append(0.5)
# 此时my_data依然是一个list列表
print('my_data的元素:', my_data)
# 对my_data应用堆属性
heapify(my_data)
print('应用堆之后my_data的元素:', my_data)
heappush(my_data, 7.2)
print('添加7.2之后my_data的元素:', my_data)
上面程序开始创建了一个 list 列表,接下来程序调用 heapify() 函数对列表执行堆操作,执行之后看到 my_data 的元素顺序如下:应用堆之后my_data 的元素:[0 , 0.5, 2, 3, 1, 5, 6, 7, 8, 9, 4]
这些元素看上去是杂乱无序的,但其实并不是,它完全满足小顶堆的特征。我们将它转换为完全二叉树,可以看到如图 2 所示的效果。
图 2 小顶堆对应的完全二叉树
当程序再次调用 heappush(my_data, 7.2) 向堆中加入一个元素之后,输出该堆中元素,可以看到如下输出结果:
添加7.2 之后my_data 的元素:[0, 0.5, 2, 3, 1, 5, 6, 7, 8, 9, 4,7.2]
此时将它转换为完全二叉树,可以看到如图 3 所示的效果。
图 3 添加 7.2 之后的小顶堆对应的完全二叉树
接下来程序尝试从堆中弹出两个元素:
# 弹出堆中最小的元素
print(heappop(my_data)) # 0
print(heappop(my_data)) # 0.5
print('弹出两个元素之后my_data的元素:', my_data)
上面三行代码的输出如下:
0
0.5
弹出两个元素之后my_data的元素: [1, 3, 2, 7, 4, 5, 6, 7.2, 8, 9]
下面代码示范了 replace() 函数的用法:
# 弹出最小元素,压入指定元素
print(heapreplace(my_data, 8.1))
print('执行replace之后my_data的元素:', my_data)
执行上面两行代码,可以看到如下输出结果:
1
执行replace之后my_data的元素: [2, 3, 5, 7, 4, 8.1, 6, 7.2, 8, 9]
print('my_data中最大的3个元素:', nlargest(3, my_data))
print('my_data中最小的4个元素:', nsmallest(4, my_data))
运行上面程序,可以看到如下输出结果:
my_data中最大的3个元素: [9, 8.1, 8]
my_data中最小的4个元素: [2, 3, 4, 5]
提示:当程序要获取列表中最大的 n 个元素,或者最小的 n 个元素时,使用堆能缓存列表的排序结果,因此具有较好的性能。
所有教程
- socket
- Python基础教程
- C#教程
- MySQL函数
- MySQL
- C语言入门
- C语言专题
- C语言编译器
- C语言编程实例
- GCC编译器
- 数据结构
- C语言项目案例
- C++教程
- OpenCV
- Qt教程
- Unity 3D教程
- UE4
- STL
- Redis
- Android教程
- JavaScript
- PHP
- Mybatis
- Spring Cloud
- Maven
- vi命令
- Spring Boot
- Spring MVC
- Hibernate
- Linux
- Linux命令
- Shell脚本
- Java教程
- 设计模式
- Spring
- Servlet
- Struts2
- Java Swing
- JSP教程
- CSS教程
- TensorFlow
- 区块链
- Go语言教程
- Docker
- 编程笔记
- 资源下载
- 关于我们
- 汇编语言
- 大数据
- 云计算
- VIP视频
